

What is a Median Triangle?
For any Triangle ABC, a median triangle is a triangle whose sides have the lengths of the three medians of Triangle ABC. A construction of such a triangle is demonstrated below.
A Construction
Start with Triangle ABC and its medians, Segments AD, BE, and CF and centroid G.
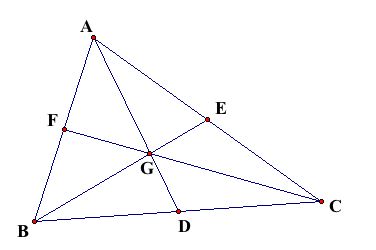 .
.
Segment FC will be the first side of the median triangle. To create the second side, Segment BE will be translated such that the image of E will coincide with C. The resulting segment is Segment HC.
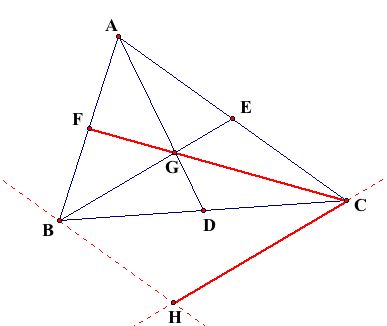
Using a similar process, Segment AD will be translated such that the image of A will coincide with F.
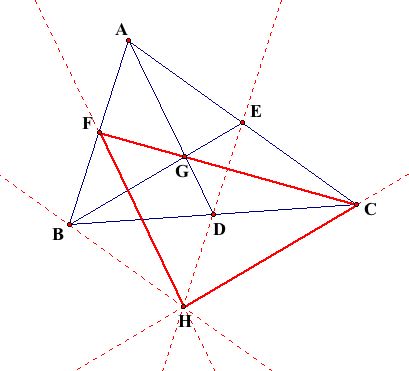
It appears that the image of Segment
AD is Segment FH. There is no proof, however, that
the image of D is indeed H from the first translation.
Until this is proved, the image of D will be called H'.
If H and H' are the same point, then the images
of B and D coincide, resulting in a triangle. By
examining vectors, this can be established.
A Proof Verifying the Translation of the Medians Results in a Triangle
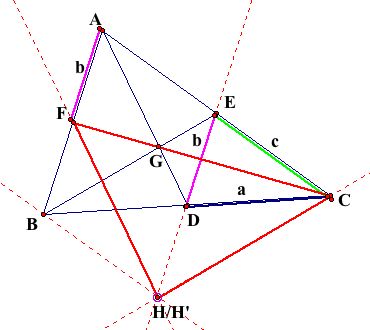
Three vectors have been established in the above figure:
Vector a, representing the direction from C to D, whose magnitude is half the length of Segment BC.
Vector b, representing the direction from A to F, whose magnitude is half the length of Segment AB. Note that Vector b could also extend from E to D, as Segment DE is the midsegment of Triangle ABC.
Vector c, representing the direction from E to C, whose magnitude is half the length of Segment AC.
Note that: Vector a + Vector b = Vector c
This leads to Vector b = -Vector a + Vector c
In the figure below, the translation of Segment BE to Segment HC is represented by the Vector c. Similarly, the translation of Segment AD to Segement BH' is represented by Vector b.
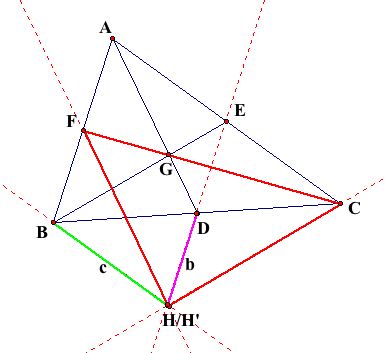
To arrive at H from D, one could travel along Vector b.
To arrive at H' from D, one could travel along the opposite of Vector a to B and then along Vector C to H'.
From the second vector equation above,
the path from D to H and the path from D
to H' arrive at the same place. Thus, H and H'
must be the same point and the construction creates the median
triangle, Triangle CFH. QED : )
The Area of the Median Triangle
Click Here.
This link will open a Geometer's Sketchpad
file containing the median triangle construction. You can use
this to explore the relationships between a triangle and its median
triangle. One such conjecture is below.
Conjecture: The area of a median
triangle is 3/4 the area of the triangle from which it was constructed.
Given: Triangle ABC and its median triangle, Triangle CFH.
Prove: The area of Triangle CFH is three fourths of the area of Triangle ABC.
For a proof of this conjecture, refer to the figure below. Let the area of the original (orange) triangle be A. To verify the above conjecture, the median triangle (green) must have an area of 3A/4.
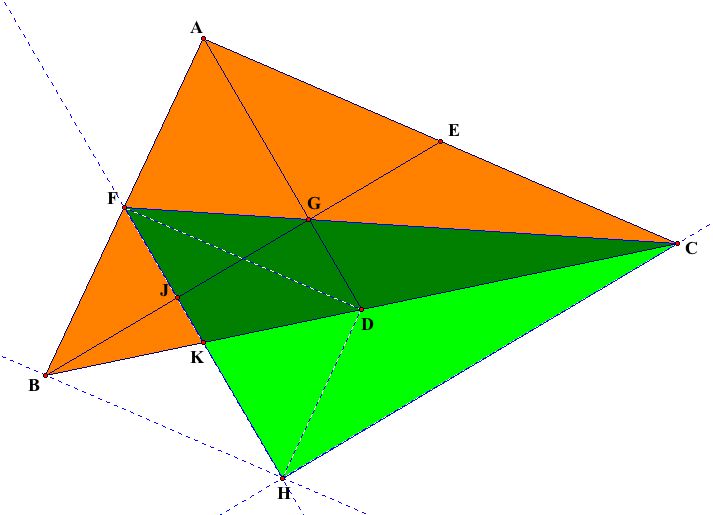
There's a lot going on here. Some things can be established right away.
Since the medians of a triangle divide it into six smaller triangles of equal area, the areas of Triangles AGE, EGC, CGD, DGB, BGF, and FGA are all A/6.
Since Segment FD is the midsegment of Triangle ABC, the area of Triangle BFD is one fourth of the area of Triangle ABC, A/4.
Since F is the midpoint of Segment AB and Line FH is parallel to Segment AD (by construction), Segement FK is the midsegment of Triangle BAD. So, Segments DK and KB are congruent making the areas of Triangles BKF and DKF equivalent and, since the triangles partition Triangle BFD, equal to A/8.
The Triangles BGF and DGB
form Qudrilateral BFGD, whose area is A/3. If Triangle
BFD, with area A/4, is removed, Triangle FGD
remains with area A/12.
The diagram below shows the area of the portion (colored dark green) of the median triangle (CFH) that overlaps the original triangle (ABC). The sum of the areas in the dark green regions is 3A/8. Note that, in order for the median triangle to have an area of 3A/4, the light green, non-overlapping portion must have the same area as the dark green portion. This can be established by showing that Segments FK and KH are congruent.
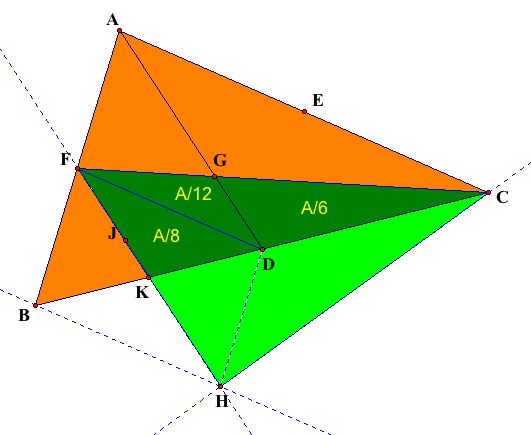
One way to show that Segments FK and KH are congruent is to show that Quadrilateral FBHD is a parallelogram. If this is the case, the diagonals of the parallelogram will bisect each other, yielding the desired congruent segments.
Since Segments DH and FB are parallel to each other (by construction), Angle FHD is congruent to Angle BFH as they are alternate interior angles. Similarly, Angle HDB is congruent to Angle FBD. Due to these congruent angle pairs and congruent segements BK and KD (from above), Triangles BKF and DKH are congruent. As a result, corresponding Segments BF and DH must be congruent.
Since segments BF and DH
are both parallel and congruent, Quadrilateral FBHD is
a parallelogram, making Segment FK congruent to Segment
KH. Thus, Triangle HKC has the same area of Triangle
FKC, 3A/8. Together, they have a combined area of 3A/4,
three quarters of the area of Triangle ABC. QED : )
What other conjectures can be made about median triangles? Can they be proved?