

What Are Tangent Circles?
For any two given circles, a tangent circle is a circle that is tangent to both circles. Some diagrams illustrating tangent circles can be found below. In each instance, the given circles are green, while the tangent circle is red.
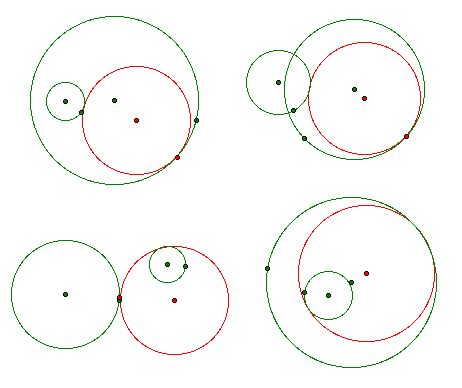
Constructions of Tangent Circles
There are many different initial conditions that could be used to construct a tangent circle. Some factors to consider are the relative size and position of the circles, as well as where the construction is to be initiated (a specified point on a particular circle) and the position of the constructed circle with respect to the given circles. These will impact the method of construction. Consider the two figures below:
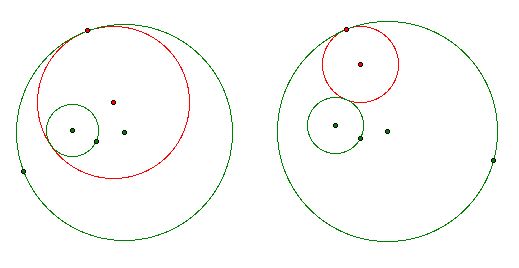
While the size and position of the given circles (green) are the same, the tangent circles are quite different. As a result of the different possibilities in the structure of tangent circles, there are many possible constructions. One of these constructions can be found below.
A Construction
Given two circles such that one circle is located in the interior of the other, construct a circle that is tangent to the larger circle at a given point and such that the non-tangent points of the smaller given circle are in the interior of the tangent circle. The above left figure depicts the goal of this construction.
.
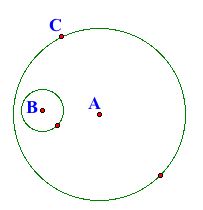
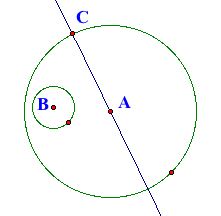
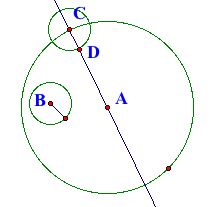
For this construction, we want the tangent circle to be tangent to Circle A at C. Circle B should be located in the interior of the tangent circle with the exception of the point of tangency. To begin the constrction, Line AC is constructed. Next, Circle C with a radius congruent to the radius of Circle B. Point D is the point of intersection of Line AC and Circle C that lies in the interior of Circle A.
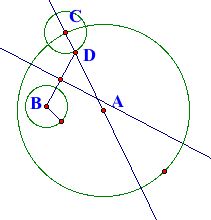
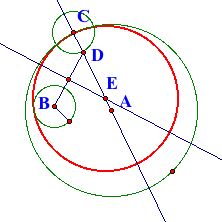
Next, Segment BD is constructed along with its perpendicular bisector. The point of intersection of Segment BD's perpendicular bisector and Line AC is E, which is the center of the tangent circle with segment AC as its radius.
Click Here to access a Geometer's Sketchpad file that has Script tools for constructing two different types of tangent circles.
The Locus of the Centers of Tangent Circles
When the point of tangency to one of the circles is changed, the position of the tangent circle is changed. As a result, the position of the center of the tangent circle also changes. If we look at a composite, or locus, of all the centers of the tangent circles, an interesting figure emerges.
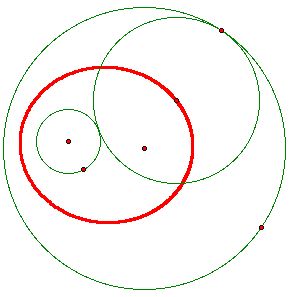
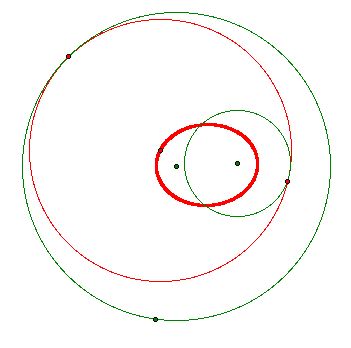
The locus is an ellipse with the foci located at the centers of the given circles. Remember that an ellipse is the set of points whose distances to two points, called the foci, sum to a constant. Can you verify this conjecture with a Proof?
Extensions
Can you complete other constructions of tangent circles?
When will the locus of the centers of the tangent circle be a hyperbola? When will the locus contain no points?