An Initial Construction
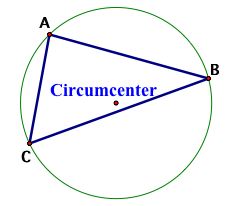
To begin this investigation, construct Triangle ABC, it's circumcenter and circumcircle. Next, construct the angle bisectors of Angles A, B, and C and the point where each bisector intersects the circumcircle. Finally, construct a triangle from these points.
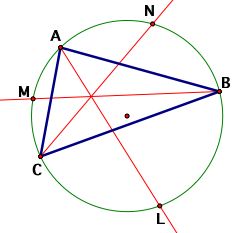
Are there any relationships between the angles in Triangles ABC and LMN?
Angle Relationship
To describe one relationship between the angles of Triangles ABC and LMN, one must establish the relative positions of the angles. If you were to trace along the circumcircle from L in either direction, the first points you will arrive at are B (if you trace counterclockwise) and C (clockwise). We will describe this relationship of Angles L, B, and C by saying that Angle L is between Angles B and C. By similar logic, Angle M is between Angles A and C, while Angle N is between Angles A and B. The following conjecture is based upon this definition:
For any two angles in Triangle ABC, the average of their measures is equal to the measure of the angle of Triangle LMN that is between them.
Some quick measurements with Geometer's
Sketchpad confirms this. Click
Here to open a sketch showing
these measures.
A Proof
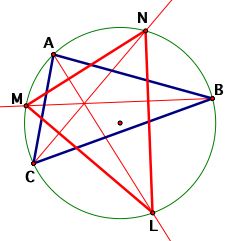
The proof of this conjecture uses the property that states: The measure of an inscribed angle is half the measure of its intercepted arc. Refer to the sketch below.
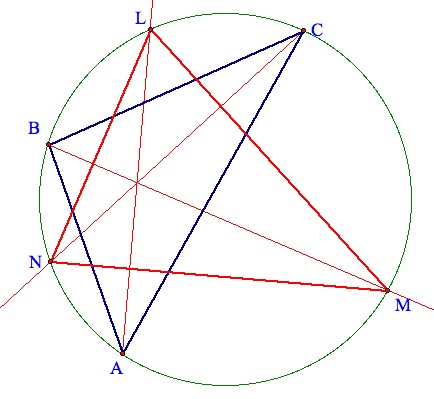
For each of the arcs listed below, assume that the minor arc (less than 180 degrees is being described).
The proof begins by showing that the measure of Angle MLN (previously called Angle L) is the average of the measures of Angles ABC (Angle B) and ACB (Angle C). Since Angle ALN and Angle ACN intercept the same arc, they must be congruent. In a similar manner, Angle ALM is congruent to Angle ABM. By the angle sum property,
m Angle MLN = m Angle ALN + m Angle ALM
Substituting in the congruent angles,
m Angle MLN = m Angle ACN + m Angle ABM
Since we know that Rays CN and BM are bisectors, then the measure of Angle ACN is half the measure of Angle ACB and the measure of Angle ABM is half the measure of Angle ABC. Thus,
m Angle MLN = 0.5(m Angle ACB + m Angle ABC)
It is indeed the average. A similar proof
can be constructed for the other two cases. QED : )
Extension
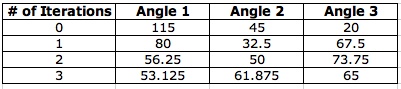
Construct another inscribed triangle using the process above and Triangle LMN as the starting triangle. If this process is repeated through many iterations, what would happen to the each newly constructed triangle and its angle measures? The spreadsheet below may give a clue. Can you prove your conjecture?