

The Pedal Triangle
The pedal triangle is a special triangle that is created with respect to a given Triangle ABC and a point P, called the pedal point. To construct a pedal triangle, refer to the diagrams below.
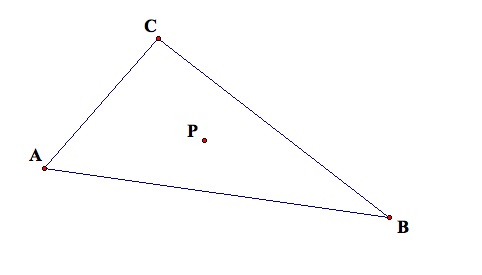
To construct the pedal triangle, a perpendicular line is constructed through each side of the triangle such that it also passes through P.
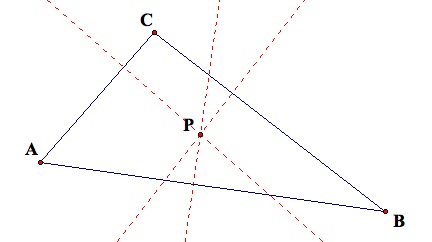
The points of perpendicularity for each side of Triangle ABC are labeled R, S, and T. Triangle RST is the pedal triangle.
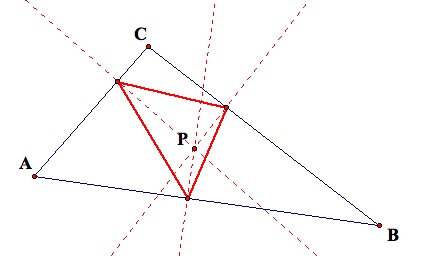
The pedal triangle has many interesting properties, many of which become apparent when the pedal point is moved to different locations with respect to Triangle ABC.
Simson Lines
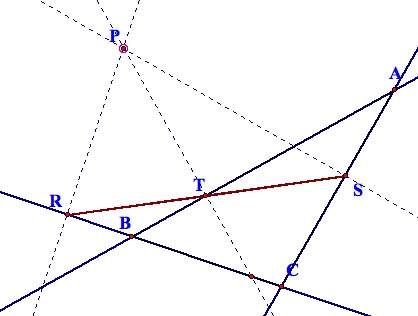
If the sides of Triangle ABC are extended, becoming lines, then the pedal triangle can be constructed for all locations of P, inside and outside of Triangle ABC. In certain locations, the pedal triangle collapses into a line segment. When this occurs, the resulting segment is called a Simson Line. An example of a Simson line is shown below.
While I spent considerable amounts of time making conjectures regarding Simson lines, I was unsuccessful at proving any of them, despite the assistance of my professor (arguably one of the smartest men in the world), his wise-beyond-years assistant, and several internet resources. So, I conclude this page with conjectures left as a challenge for the visitor to prove. Please Email Me! if you have any success.
Some Unproved Conjectures
1. If the pedal point P lies on the circumcircle of Triangle ABC, then the pedal triangle is a Simson line.
Click Here to download a Geometer's Sketchpad file containing a sketch related to conjecture #1.
2. Given the pedal point is on the circumcircle of Triangle ABC. Then the midpoint of the pedal point and the orthocenter of Triangle ABC is on the Simson line
Click Here to download a Geometer's Sketchpad file containing a sketch related to conjecture #2..
3. Given conjecture #2, the locus of these midpoints is the nine-point circle of Triangle ABC.
Click Here to download a Geometer's Sketchpad file containing a sketch related to conjecture #3. (Note, the construction, for some reason, omits part of the nine-point circle, which has been vexing me as well. Email Me! if you know what is wrong.)
set of equations does not graph the entire unit circle, can you show why it doesn't?