

Parametric Equations
Parametric equations are useful in graphing curves that cannot be represented by a single function. In parametric equations, each variable is written as a function of a parameter, usually called t. For example, the parametric equations below will graph the unit circle (t = [0, 2*pi]).
x = cos(t)
y = sin(t)
At t=0, x = cos(0) = 1 and y = sin(0) = 0, or (1, 0). As t increases, each new value of t will provide another point on the unit circle. By the time t = 2*pi, the circle will be complete.
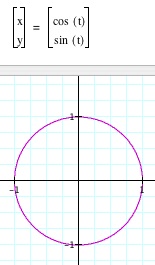
It can be easily proved that this set of equations will produce the unit circle. Consider the proof below.
We know the proof of the unit circle below. By simple squaring x and y, one of the fundamental Pythagorean trigonometric identies is revealed. Since this structure equals 1, we arrive at the equation for the unit circle.
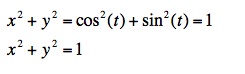
Another Set of Parametric Equations
Consider the following parametric equations:
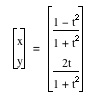
When this set of parametric equations is graphed with t=[-pi,pi], the curve is also circular. Notice the circle is incomplete. Click Here to open a Graphing Calculator file for this set of parametric equations. What happens as you change the range for t?
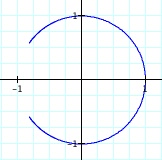
Two questions arise from the this set of parametric equations and their graph:
1. Why is it circular?
2. Why does only part of the circle appear?
Proof of Circularity
A proof similar to the one above will establish that the graph is indeed circular.
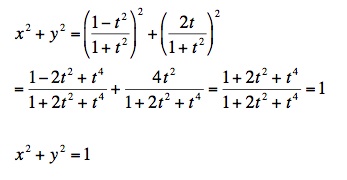
The Partial Circle
The partial circle is due to the nature of these particular parametric equations. In order for the circle to be completed, the remaining arc, that includes the point (-1, 0) must be graphed. In examining the equation for x, it becomes evident that it can never equal -1.
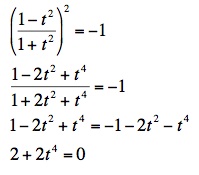
Furthermore, it can be established that y can only equal zero when t equals zero.
As we increase the bounds of the interval for t, more of the circle is graphed. The circle, however will never be completed. An analysis of the limits of x and y as t grows without bound reveals that the curve will approach (-1, 0).
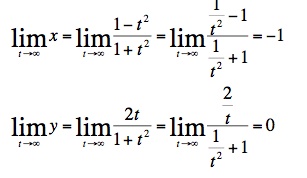
Similar limits can be calculated as t approaches negative infinity.
Challenges
Can you find another set of parametric equations whose graph is the unit circle (or part of it)? Can you prove that your equations are circular? If your set of equations does not graph the entire unit circle, can you show why it doesn't?