

The Fibonacci Sequence
The Fibonacci Sequence is a pervasive mathematical concept, appearing in a variety of mathematical and nonmathematical contexts. For a brief history of its origin, Click Here. It is generated by choosing the values of the first two terms. Classically, the first terms are set equal to 1. The third term (and each successive term) is calculated by adding the two terms immediately preceding it. Thus, using 1 as the value for the first two terms, the Fibonacci Sequence is as follows:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
The Fibonacci Sequence can be easily
created on a spreadsheet. To open a Microsoft Excel file containing
the Fibonacci Sequence, Click
Here.
Ratios of the Fibonacci Sequence
Some interesting relationships occur when various ratios between terms of the Fibonacci Sequence are calculated. One popular ratio is that between consecutive terms. The figure below shows the ratios between consecutive terms of the Fibonnaci Sequence.
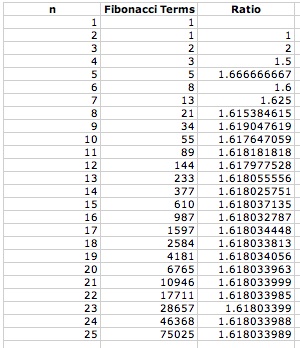
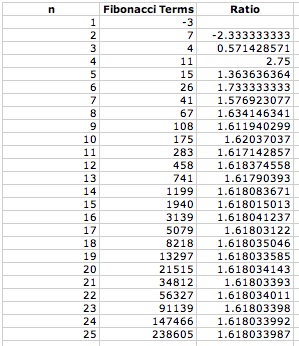
Note that, as the value of n increases, the ratio between consecutive terms approaches phi, the Golden Ratio. This phenomenon occurs no matter what non-zero values are chosen for the first two terms. For example, the terms -3 and 7 are used in the figure below with a similar result.
Why does the ratio of consecutive Fibonacci
terms approach phi as n increases? Click
Here for a brief explanation.
Other Ratios
There are other interesting ratios found with terms from the Fibonacci Sequence. For instance, what if the ratio of every other term is calculated? The spreadsheet can perform these calculations quickly, as seen in the figure below.
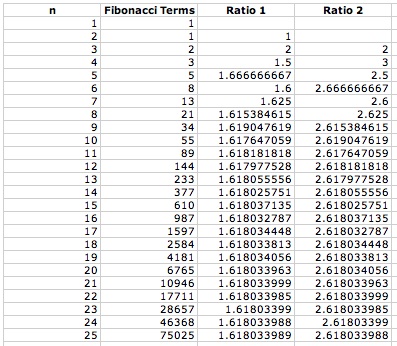
It appears that, as n grows larger, the ratio between every other term of the Fibonacci Sequence approaches phi + 1. This expression is equivalent to phi squared. An explanation of this relationship can be found below.
Using the notation and result of the consecutive terms explanation, the equation below show that the ratio between every other term approaches phi + 1.
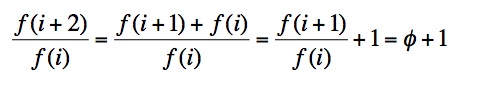
The equation below demonstrates that phi + 1 equals phi squared.
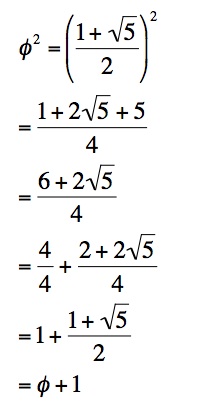
Is it possible to generalize this result to other ratios? That is, would the ratios of every third term of the Fibonacci Sequence approach phi to the third power? It would appear so.
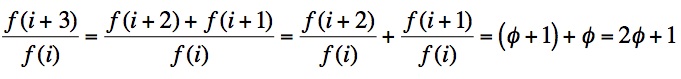
An algebraic argument similar to the one above will establish that this result is equivalent to phi cubed.
Challenge
Can these proofs be generalized to incorporate the ratios between every nth term of the Fibonnaci Sequence? Click Here for one possible way of beginning.