

The Problem
Find as many solutions as possible to the following system of equations:
ABC = 4
3A + 2B - C = 3
This is a system of equations with three
variables but only two equations. More likely than not, it will
have multiple solutions.
Strategy #1: Algebra!
My initial strategy was to approach the system algebraically. Using the substitution method, I arrived at three equations that describe sets of solutions.
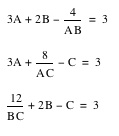
While these equations are quite nice,
they do not reveal much about the nature of the solutions or how
A, B, and C interact with each other.
Strategy #2: Graphs in Two Dimensions
To get a better idea of the relationships between the three, I graphed the equations in two-dimensions. In order to effectively use the Graphing Calculator software, I let A=x, B=y, and C=z. The graphs can be seen below.
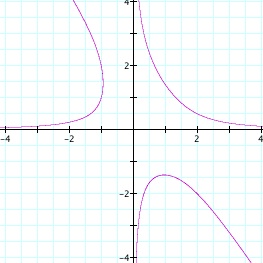
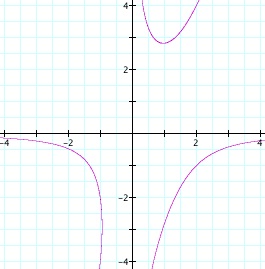
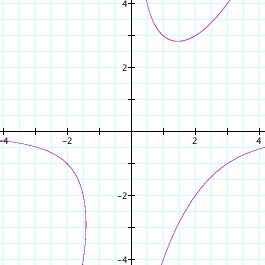
The graphs of the solution on the xy, xz, and yz planes, respectively.
These graphs showed the interaction between the variables a little bit better. Upon viewing these, I observed that none of the three variables can equal zero as there are no intercepts with any of the axes. This makes sense given the first equation of the system. Another observation is that certain quadrants are empty, indicating that there are combinations of signs for variables that are not permitted:
x and y can't both be negative (from the first graph)
x can't be negative while z is positive (second graph)
y can't be negative while z is positive (third graph)
These rules indicate that, if the system
were to be graphed in three dimensions, certain octants would
be empty.
Strategy #3: Three-Dimensional Graph
To create a three dimensional model of the system with Graphing Calculator, I graphed each equation separately to get a sense of their individual properties. The graph for xyz = 4 is graphed below in red. It has four distinct regions located in the first octant, the top-left-back octant, the bottom-left-front octant, and the bottom-right-back octant. The graph of 3x + 2y - z = 3 is graphed in blue. It is a plane.

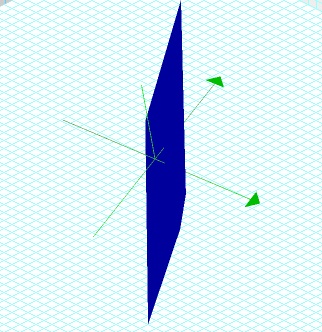
By examining both equations graphed on the same set of axes, the solution to the system can be analyzed. Click Here to download a Graphing Calculator file with the graph of the system. Some views of this graph can be seen below.
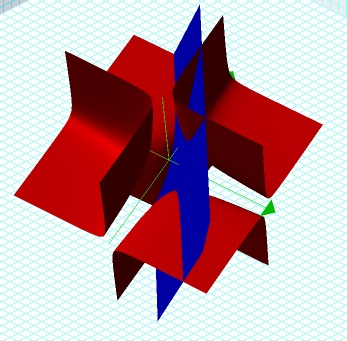

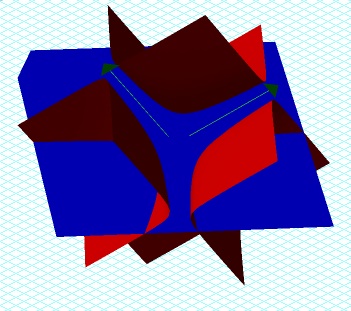
Can the conjectures made regarding the 2-dimensional graphs be verified? Clearly from looking at the graph of the first equation (in red) that none of the three coordinates equal zero. The graph does not touch any of the axes. With regard to the rules about the signs of the coordinates, they are restated below along with a 3-dimensional justification.
x and y can't both be negative - This is clear from the first graph of the system, which is looking down on Quadrant III (furthest left). Notice the two graphs never intersect here.
x can't be negative while z is positive - This is also apparent from the first graph. The only solutions of the system located above the xy-plane are above Quadrant I (furthest right) where all three variables are positive.
y can't be negative while z is positive
- See the second explanation.
Extensions?
What other conjectures can be made about the solution to this system? Can you prove them?