

Stamp Prices
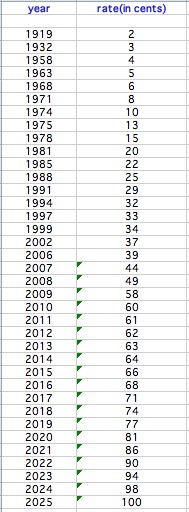
This data set below is based on the first class letter postage for the US Mail from 1933 to 2006.
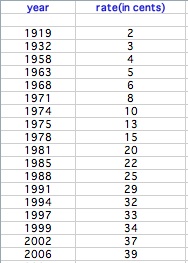
Notice that the price of a first class stamp increased infrequently during the half of the 20th century. The 1960's marked the beginning of more frequent increases. This trend becomes readily apparent when the data is viewed as a graph.
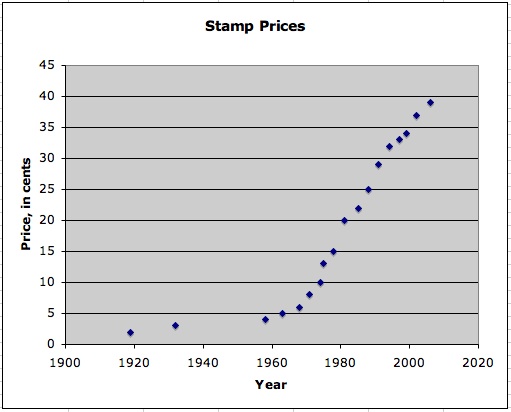
In order to use this data to predict the price of stamps for a given year or the year stamps had a particular price, consideration must be given to the fact that the price does not behave in a linear fashion across the entire data set. If a best-fit line was approximated for the data, it would look like this:
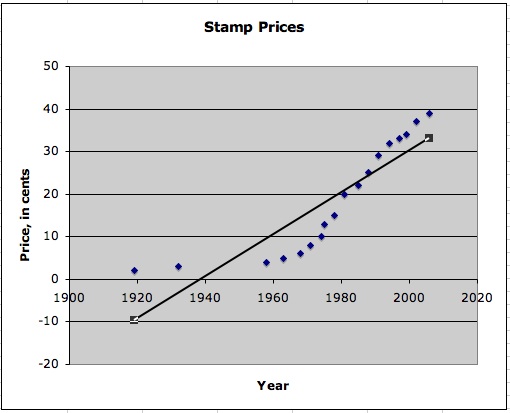
Does this line approximate the data well?
Would it accurately predict future prices? Probably not.
Other Options
Other types of non-linnear curves can be used to approximate a set of data. For instance, a curve approximating the above stamp data could be exponential:
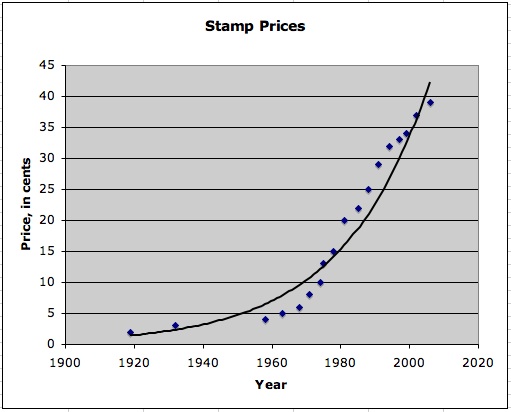
This curve appears to provide a better
fit for the data.
Making Predictions
The (exponential) GROWTH function of Excel can now make predictions about missing data. First, values must be generated to represent the future.
Consider the following questions:
When will the price of a postage stamp reach 74 cents?
When will it reach $1.00?
According to the exponential model created for stamp prices, the answers are 2018 and 2025, respectively. The important questions to now ask are:
Do you believe this model is valid (are the predictions accurate)? Why?
Why is the price of a stamp increasing
so rapidly?
Another Possibility...
Notice that the data behaves "more linearly" by removing the early data points from the set (say earlier than 1968).
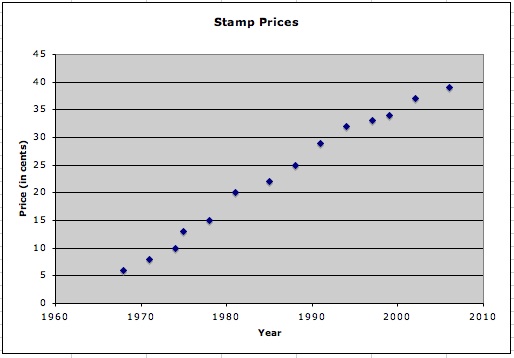
To use this data, there must be justification for omitting part of the data set. Perhaps fuel prices were stable prior to 1968, or postal worker salaries began increasing around this time due to union activity, or...
By using a linear regression, the following data is generated:
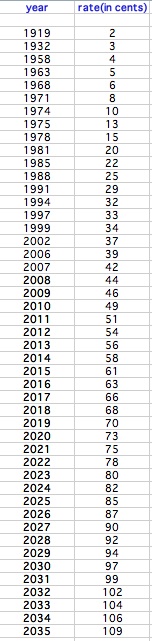
This leads to different answers to the questions: 74 cents in 2021 and $1.00 in 2032
Which is the correct model? Determining and justifying that decision is part of doing mathematics!