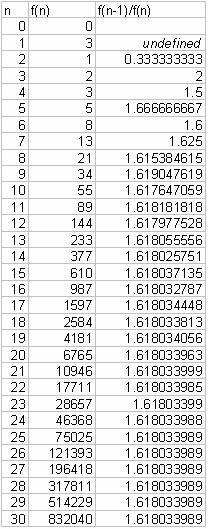
Michael Thomason's write-up for assignment twelve, question four.
Generate
a Fibonacci sequence in the first column using f(0) = 0, f(1) = 1, f(n) =
f(n-1) + f(n-2).
The first two numbers are called seeds. Using different
seeds changes the sequence, but we will see that the ratio between each
iteration (step) and the one before it tends to the same number regardless of
which two seeds are used.
Here I have created an Excel worksheet that calculates
the first several iterations for the indicated seeds. You may open it by
clicking here; change
the seeds and press enter to see what happens to the sequence.
The first Fibonacci sequence in the above table is
quite well-known and is shown here:
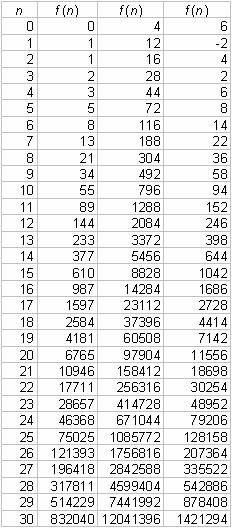
Do the above numbers increase by a proportion
determined by the seeds, or does their progression continue by the same proportion
regardless of the seeds chosen? Here is another Excel spreadsheet, this time
with the ratio between each step displayed:
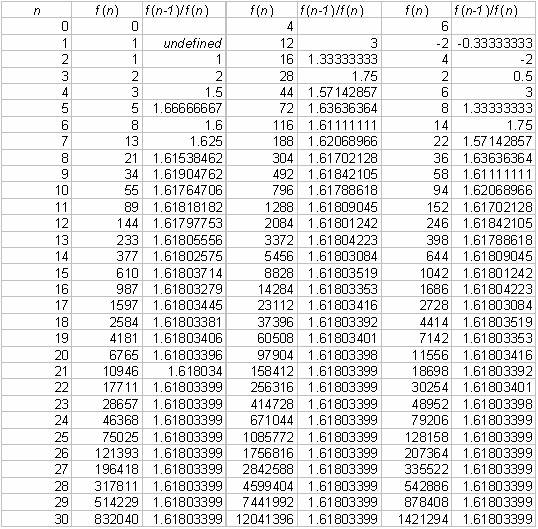
(Click here to change the seeds and
observe how 
behaves.)
For all three sequences, the value for tends to the same
number, 1.61803399. This number is called the golden ratio, and is exactly
expressed as 
. Click here to see the first 5000
digits of the golden ratio, which is also called 
(phi).
This sequence, for which the seeds are f(0)=1 and f(1) = 3, is called a Lucas sequence. It too has values for tending to .
