Michael Thomason's write-up for assignment three, investigation one.
![]() is the general
form of the equation for a parabola (with a , b , and c
constants) along with the graphs for a = c = 1 and b = {-3, -2, -1, 0, 1, 2, 3}:
is the general
form of the equation for a parabola (with a , b , and c
constants) along with the graphs for a = c = 1 and b = {-3, -2, -1, 0, 1, 2, 3}:
> plot([x^2-3*x+1,x^2-2*x+1,x^2-1*x+1,x^2+1,x^2+1*x+1,x^2+2*x+1,x^2+3*x+1],x=-5..5,y=-2..5,color=[blue,yellow,black,green,red,coral,khaki]);
![[Maple Plot]](images/assignment32.gif)
As b goes from -3 to 3, the vertex of the graph "moves" while the rest of the graph seems to maintain its curvature relative to its vertex. Do the vertices travel along a set path? Let's find the coordinates for the vertex. Taking the derivative of f ( x ), setting it equal to zero, and solving should give the x -coordinate of the vertex, which can then be used to find the correspondng y -coordinate.
> f:=x->x^2+b*x+1;
D(f)(x);
solve(D(f)(x)=0,x);
f(solve(D(f)(x)=0,x));
![]()
![]()
![]()
![]()
So
the coordinates of the vertex for this case of ![]() , namely when a
= c = 1, are (
, namely when a
= c = 1, are ( ![]() ,
, 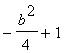 ). So then, what path does the vertex trace? ie, What is the locus of the
vertices of the parabolas? From the coordinates here we have:
). So then, what path does the vertex trace? ie, What is the locus of the
vertices of the parabolas? From the coordinates here we have:
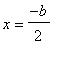
![]()
![]()
Plug into the y -coordinate:
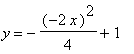
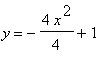
![]()
Now let's graph this along with the graph from before (the locus is colored differently from the parabolas):
> plot([x^2-3*x+1,x^2-2*x+1,x^2-1*x+1,x^2+1,x^2+1*x+1,x^2+2*x+1,x^2+3*x+1,-x^2+1],x=-5..5,y=-2..5,color=[blue,blue,blue,blue,blue,blue,blue,khaki]);
![[Maple Plot]](images/assignment316.gif)
![]() does indeed trace the vertices of the graphs of
does indeed trace the vertices of the graphs of ![]() . What traces the vertices of the graphs of
. What traces the vertices of the graphs of
![]() ? Let's follow the
steps from before and see.
? Let's follow the
steps from before and see.
> f:=x->a*x^2+b*x+c;
D(f)(x);
solve(D(f)(x)=0,x);
f(solve(D(f)(x)=0,x));
![]()
![]()
![]()
![]()
So the
coordinates of the vertex for the general form of a parabola, ![]() , are (
, are ( ![]() ,
, 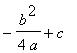 ). We can follow the steps from the previous case to see
the general equation for the locus of the vertices of the parabolas:
). We can follow the steps from the previous case to see
the general equation for the locus of the vertices of the parabolas:
![]()
![]()
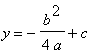
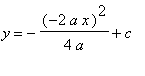
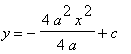
![]()
So
the locus of the set of vertices of the set of parabolas given by ![]() is the parabola
is the parabola ![]() . Here is a graph for
. Here is a graph for ![]() , and b = {-15,
-10, -5, 0, 5, 10, 15} (the locus is colored differently from the parabolas):
, and b = {-15,
-10, -5, 0, 5, 10, 15} (the locus is colored differently from the parabolas):
> a:=3;c:=6;y:=x->-a*x^2+c;plot([y(x),3*x^2-15*x+6,3*x^2-10*x+6,3*x^2-5*x+6,3*x^2+6,3*x^2+5*x+6,3*x^2+10*x+6,3*x^2+15*x+6],x=-5..5,y=-20..20,color=[khaki,blue,blue,blue,blue,blue,blue,blue]);
![]()
![]()
![]()
![[Maple Plot]](images/assignment339.gif)
Here is another graph, this time with a = -2, c = 4, and b = {-6, -4, -2, 0, 2, 4, 6} (the locus is colored differently from the parabolas):
> a:=-2;c:=4;y:=x->-a*x^2+c;plot([y(x),-2*x^2-6*x+4,-2*x^2-4*x+4,-2*x^2-2*x+4,-2*x^2+4,-2*x^2+2*x+4,-2*x^2+4*x+4,-2*x^2+6*x+4],x=-3..3,y=-5..10,color=[khaki,blue,blue,blue,blue,blue,blue,blue]);
![]()
![]()
![]()
![[Maple Plot]](images/assignment343.gif)
So,
I have found the locus of the set of vertices of the set of parabolas given by ![]() to be the parabola
to be the parabola ![]() . I have also checked a couple cases and graphed them.
. I have also checked a couple cases and graphed them.