Michael Thomason's write-up for assignment four, problem twelve.
12. Prove that the three perpendicular bisectors of the sides of a triangle are concurrent.
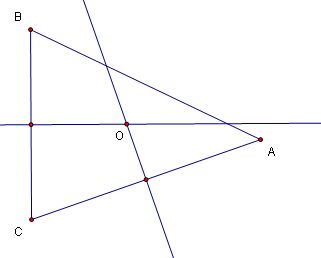
I will begin by constructing a triangle with two sides having their perpendicular bisectors drawn. They intersect at a point called the circumcenter, labeled O. I know they always intersect because they are perpendicular to lines with different slopes, so they too have different slopes and therefore must intersect. Click the drawing to open a GSP file; move the vertices of the triangle as you wish and note that the two perpendicular bisectors always intersect.
Claim: The
perpendicular bisector of 
also passes also
through O.
Proof: O lies
on the perpendicular bisector of 
, so O is equidistant from A and C, i.e.
. Likewise,
. Substitute to see that 
, which implies that O lies on the perpendicular bisector of .
Therefore, the
three perpendicular bisectors of the sides of a triangle are concurrent.
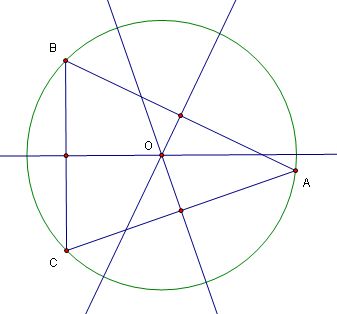
Moreover, it has been shown that 
, i.e. that O is the circumcenter of triangle ABC. Click
below to open a GSP file showing O and the circumcircle; move the vertices of
the triangle as you wish and note that O is the center of the circumcircle of
the triangle and that the three perpendicular bisectors are indeed concurrent
at O.
