Michael Thomason's write-up for assignment six, exploration seven.
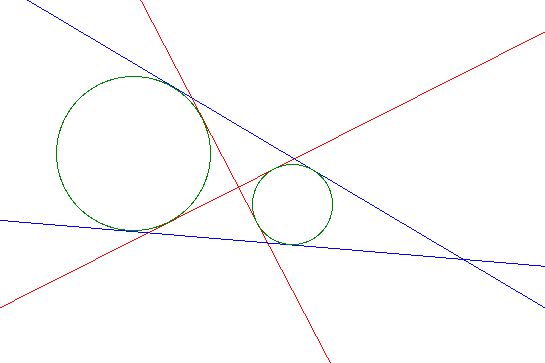
Given two circles, it is possible to construct four common tangents to the two circles as shown here:
(click to open GSP file).
The pair of blue lines can be drawn with one construction, and the pair of red lines can be drawn with their own construction, which is similar to that for the blue lines. I will begin with the construction for the blue lines.
A line tangent to a circle is perpendicular to the circle's radius at the point of tangency, so a line that is commonly tangent to two circles will be tangent to parallel radii (one radius from each circle). The first step in this construction is to construct two parallel radii:
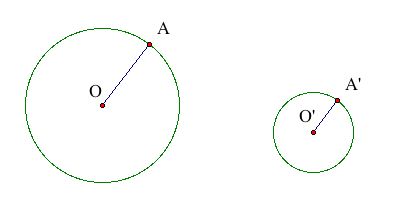
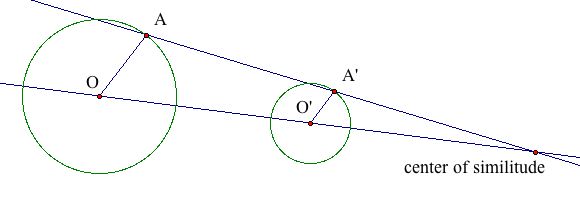
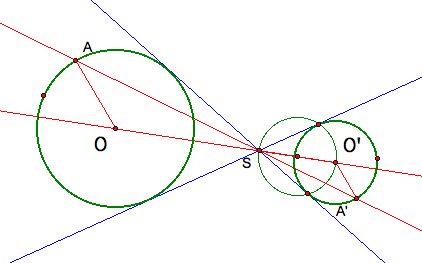
The next step is to connect O and O' with a line and A and A' with a
different line. The intersection of these two lines is called the external
center of similitude, which is shown here. Click to see how the center of
similitude remains static regardless of the location of A and A' on their
respective circles:
I will now construct the midpoint of the segment O'S (S is the center of similitude) along with the circle centered at this midpoint passing through S and O'.
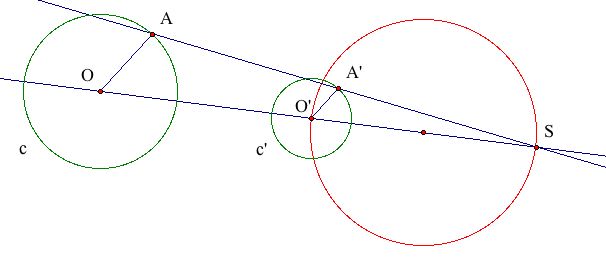
The line passing through S and the intersection of the circle c' with the
red circle will be tangent to the circle c'. (I have chosen the northern
intersection between c' and the red circle for neatness, but the line through S
and the southern intersection is also tangent to c'.)
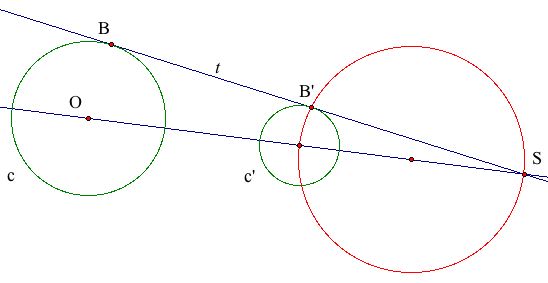
The tangent line t is also tangent to c at the point B. Drawing in
the other tangent line and hiding the red circle, the points B, B', and S, and
the line OS gives this picture:

(click above to load the GSP script tool for this construction; to use the
script, create two circles, load the script tool "Common Tangents 1,"
and then - in order - click the first circle's center, the first circle, the
second circle's center, and the second circle).
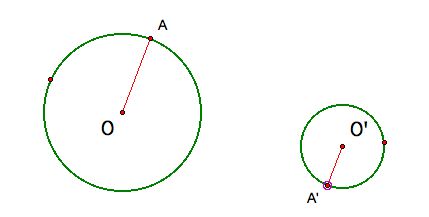
The other two tangent lines, originally colored red, are constructed by a
similar method. Start with two circles, each with a parallel radius drawn.
Unlike before, draw the radii this way:
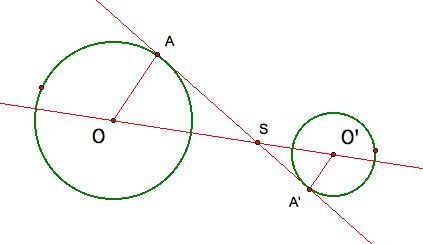
Now draw the lines OO' and AA' and find the internal
point of similitude.
Construct the midpoint of O'S and a circle centered at that midpoint with
diameter O'S.
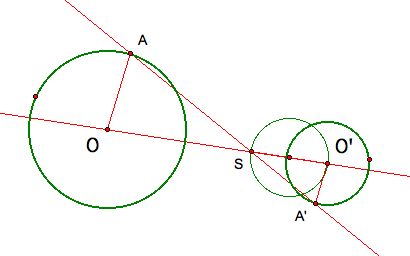
This new circle intersects the circle centered at O' in two places. The
respective lines through those points and the point S are the other two tangent
lines, which are colored blue here.
(click above to load the GSP script tool for this construction; to use the
script, create two circles, load the script tool "Common Tangents 2,"
and then - in order - click the first circle's center, the first circle, the
second circle's center, and the second circle).