Michael Thomason's write-up for assignment seven.
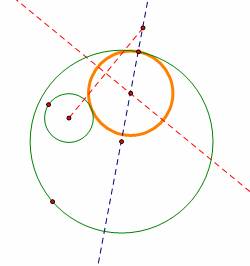
Given two circles like this, I will show a construction for a third circle which is tangent to both original circles:
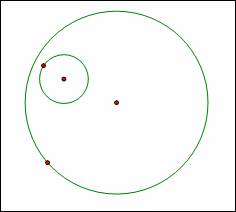
I begin by drawing a line through the center of the larger
circle like so:
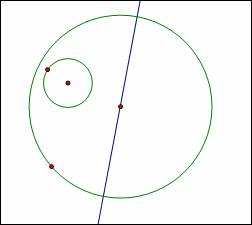
I will now construct a circle centered at an intersection of the line with the larger circle, the new circle having radius equal to the smaller circle. Also constructed is the intersection of the line with the new circle which is outside the large circle:
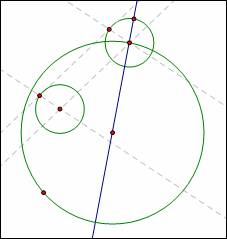
Now I construct the red segment as shown along with its perpendicular bisector:
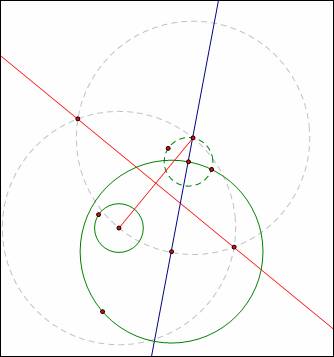
The circle tangent to the solid green circles is centered at the intersection of the red and blue lines, as shown here:
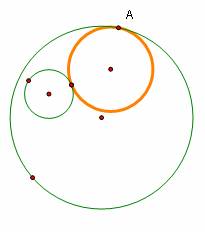
Click here to open a GSP file with
the above circles. Move the green circles around and see how the orange circle
remains tangent to both of them. There is a script tool included in the file
called “Tangent circle” that will complete this construction. Note
that the script creates the first circle (the one without tangency point A)
first.
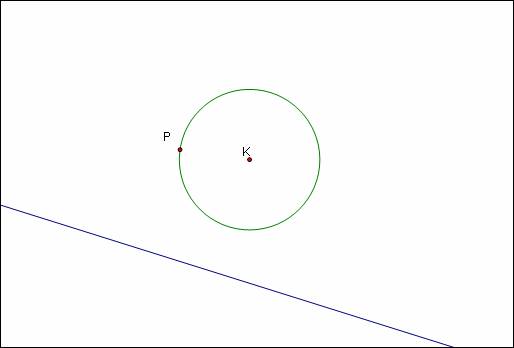
Investigation: Given a line and a circle with center K. Take an arbitrary point P on the circle. Construct two circles tangent to the given circle at P and tangent to the line.
I begin by drawing the given items:
I now construct the line perpendicular to the circle at point P. Both of the tangent circles will be tangent to this line at the point P too.
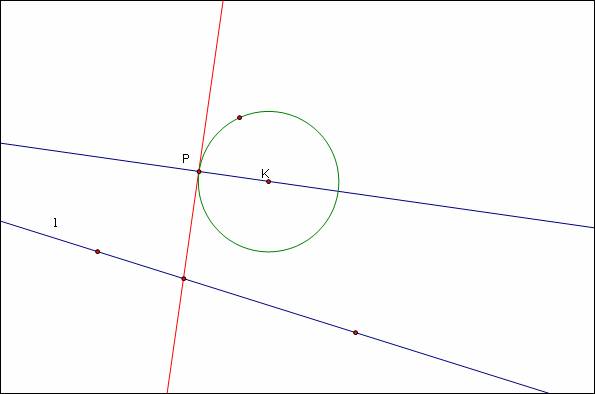
The angle bisectors
between l and the red line will come
in handy:
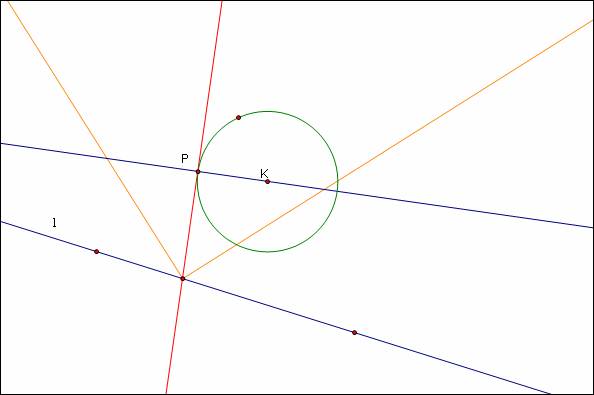
The intersections between the angle
bisectors and the line 
are the centers
of the two tangent circles. Click here to check this out in GSP.
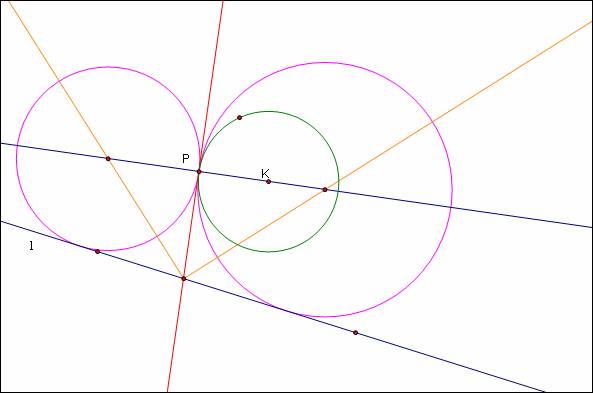
Why does this construction work? The two tangent circles must be tangent to the line tangent to the original circle at the point P. The tangent circles must also be tangent to the line l. Let’s look at a close-up of the tangent circle at left:
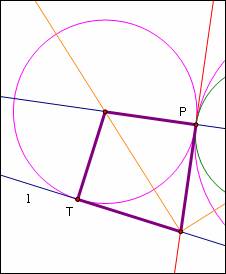
So, we have a kite with right angles at the points P and T. We wanted these right angles because they are equivalent to tangency between the tangent circle and the other items at the points P and T. We needed the angle bisector to ensure that the tangent circle’s radii that form two sides of the kite are of equal length. The angle bisector does this by creating two congruent right triangles which together form the kite.
What is the locus of the centers of the tangent circles as P moves around the original circle? Here is a picture. You can click here to watch the animation that created it.
