Michael Thomason's write-up for assignment nine, question seven.
Let
triangle ABC be any triangle. Then if P is any point in the plane,
then the triangle formed by constructing perpendiculars to the sides of ABC
(extended if necessary) locate three points R, S, and T that are the
intersections. Triangle RST is the Pedal Triangle for
Here are a few pictures of the pedal triangle RST for
a fixed triangle ABC with P in different locations:
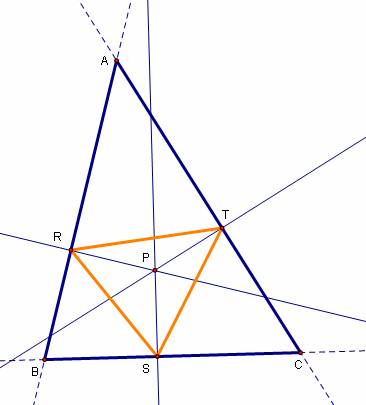
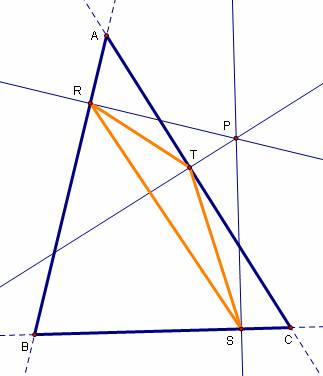
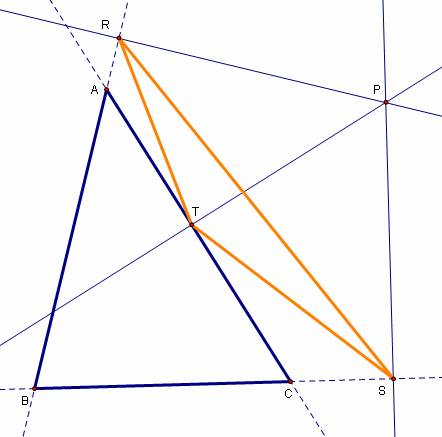
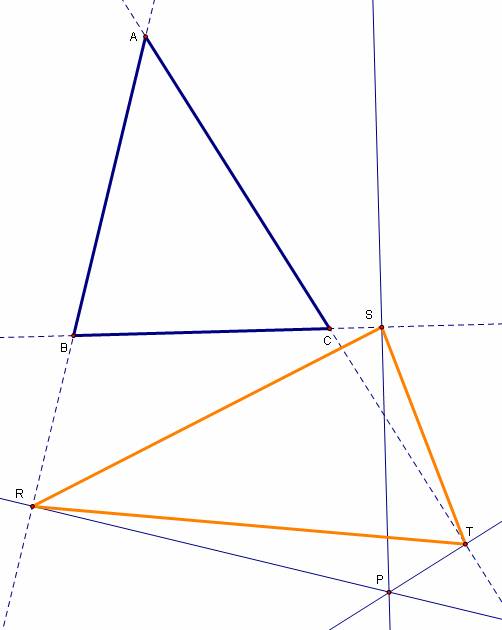
Click here to open a GSP file with the
above triangle and pedal triangle. See what happens when you move P to various
locations. There is also a script tool called “Pedal Triangle” that
will construct the pedal triangle for a given triangle and pedal point.
What if P is on a side of the original triangle? Here
are a few pictures:
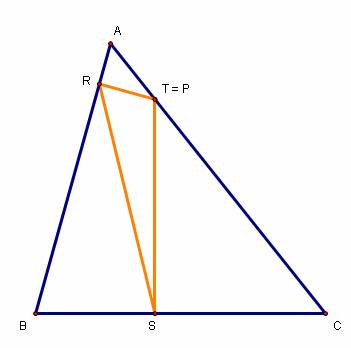
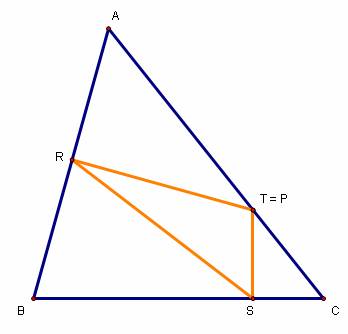
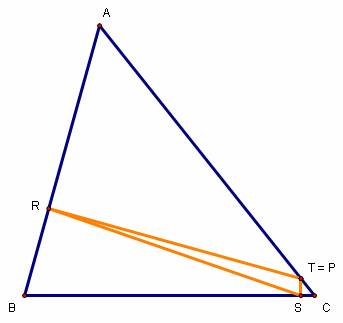
The angle RPS remains the same regardless of P’s
position along 
. In addition, RPS + ABC always equals
180˚. Click here to see an animation that
shows this. Note that RPS + ABC always equals 180˚
even if you change the location of points A, B, and/or C.