Part A

Bouncing Barney

by Margaret Trandel

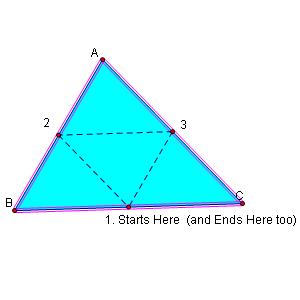
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point.

 

Let's first take a look and see if Barney makes it back to his starting point. Follow Barney's path by following the numbers.

When Barney starts at the midpoint of side BC and follows the path outlined above, he indeed ends up at his starting point.

In the two cases below, Barney also ends up at his starting point.

 

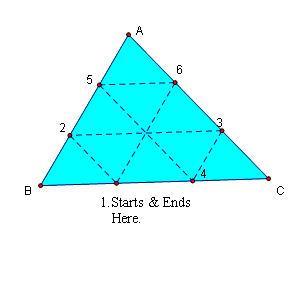
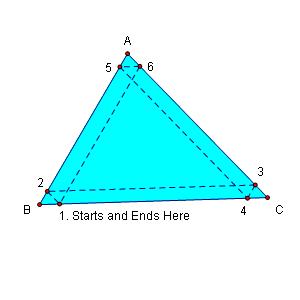
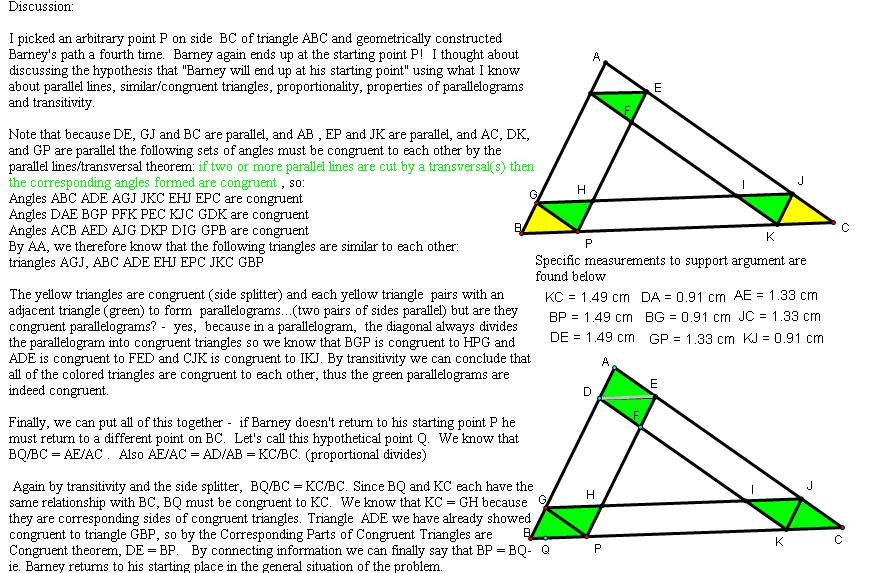
This of course is not a proof that Barney will end up at his starting point every time. Let's look at an arbitrary case, analyze and prove.