
Part B
Multiple Solutions
1. Find as many solutions as possible for X, Y, and Z that satisfy both equations:
3X + 2Y - Z = 3.
Before graphing the equations above I thought about some possible solutions, First of all I used the first equation to rule out zero as a possible solution.(Obviously if the right side of an equation is four, zero cannot be a factor.) Next I played around with some simple integer values and using guess and check, came up with the solution (-1, 2 -2). There is at least one solution to the system above, and most likely a whole lot more!
Next I thought it would be interesting to graph the equations in three variables. This is fun for me, as all of my technological graphing to date has only been in x and y. Look below to find three variable graphs:
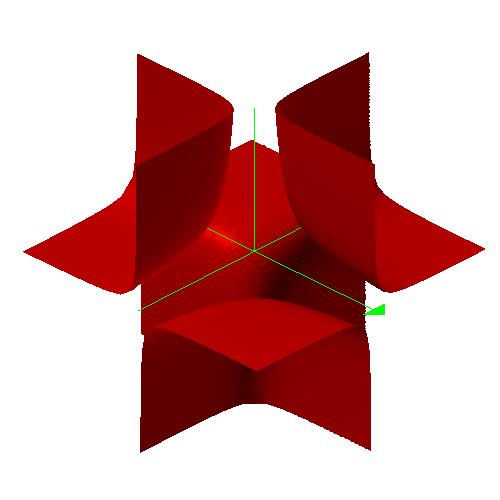
The graph of the next equation is going to be that of a plane. It appears as the two graphs will intersect uncountable times.

Now let's graph the equations simultaneously and see if our conjecture is correct.

Bingo...many, many intersections.
Obviously, the graphs intersect, but where? My idea is to write the equations in x and y and use graphing techniques I am familiar with solve for x and y. Once we have x and y, we can plug the values into the original equations to solvc for z.
Given the two original equations, what if we solve for z in in the first equation (z=4xy) and substitute for z in the second equation. Then we will have a two variable equation.
Equation in x and y = 3x2y + 2xy2 - 3xy = 4
You'll find the algebra below:
xyz = 4, so z = 4/(xy)
3x +2y - 4/(xy) = 3
3x2y + 2xy2 - 4 = 3xy
3x2y + 2xy2 - 3xy = 4
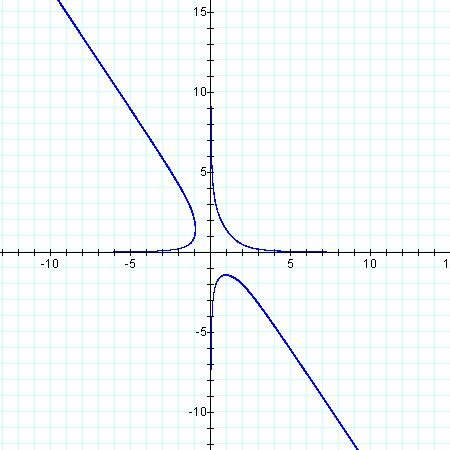
By examining the graph above we can see that there are not solutions where x and y are both negative.
By examining our graph we can also find many solutions to our equations. The solutions are obviously infinite. Let's examine a couple of values for x and y on the graph. For instance, (-1, 2 ) are on the graph. Now if we plug -1 in for x and 2 for y into our original equations, we find that z = -2, so (-1, 2, -2) is a solution. Another point on our coordinate plane graph is (2,1/2) If we again plug these values in for x and y in to our original equations z must be 4, so the solution is (2, 1/2, 4)