
Final Part C
Postage Stamp Activity
The Ever-changing Price of a U.S. Postage Stamp
by Margaret Trandel
In this assignment I used Excel to record the price of the U.S. postal stamp from 1919 to 2006. How apropos I am working on this assignment today, as at midnight tonight the price jumps to from .37 to .39 to mail a first class letter! Thank goodness for e-mail!
Using Excel, I will find a regression equation and make predictions to answer the following questions:
When will the cost of a first class postage stamp reach $1.00?
When will the cost be 74 cents?
How soon should we expect the next increase?
(In 1996, the analysis of stamp data historically seemed to show that the postage doubled approximately every 10 years. The cost in 2006 would seem to argue that pattern is no longer valid.) Is there evidence to show a change in the growth pattern? Or, was the 'doubles every ten years' just a bad model?
Stamp Prices
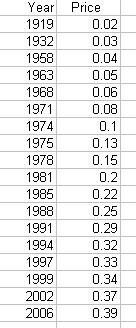
Here is a scatter plot of the stamp data. As you can see, the data appears to fit an exponential model. In an exponential model, as x becomes larger, y continues to increase at a growing rate. This fits our model. For example, between 1919 and 1958, stamp prices only increased by two cents, and in the past two years alone stamp prices have gone up by two cents!
To find our exponential equation of best-fit, we can use the TI-83 Graphing Calculator or Excel. Since I am familiar with the graphing calculator method, I decided to learn about the Excel graphing and regression features. Below you will find the Excel Scatterplot, Exponential Equation of Best Fit, and and the graph of the Exponential Equation.
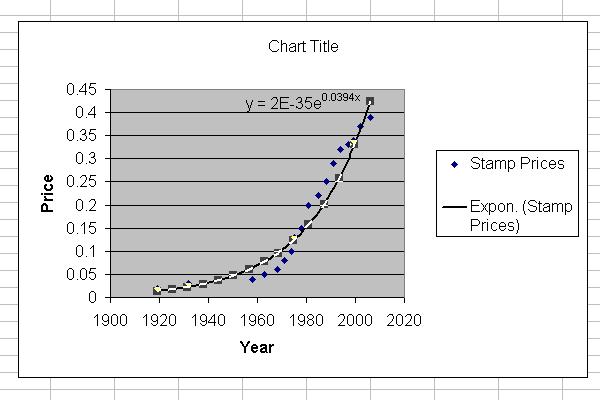
The equation for our data (for price in dollars) is:
y = 2E-35e.0394x
Let's use this equation to predict future stamp prices. I made a new chart below and included the predicted postage rates through the year 2028, when stamp prices reach a dollar according to the model.
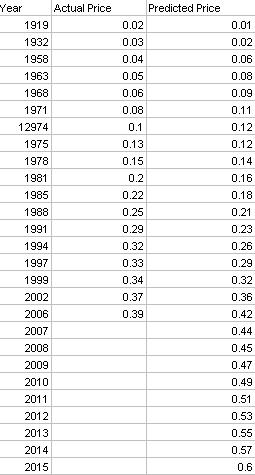
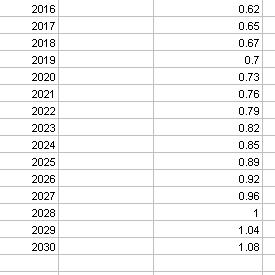
As you can see, based on my model the price of a stamp will reach $1.00 in 2028. The price will be $.73 around 2020.
The exponential model seemed roughly accurate at first, with prices doubling every ten years or so. However, as time has passed, stamp prices now seem to be increasing at a slower rate than an exponential model predicts.