Assignment 3

Problem #1

by Margaret Trandel

 

The general form of a quadratic equation is: y = a x²+ bx +c. This investigation will discuss the movement of the quadratic graph as b changes value. In the equations below, b is an integer such that -4 < b < 4, and a and c each remain constant at a = 1 and c = 1 in all of the equations. Looking at a graph of the quadratic equations below, we can see some similarities.

 

   

   

   

 

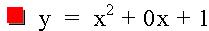
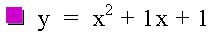
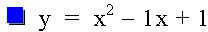
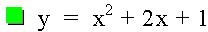
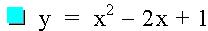
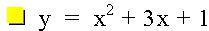
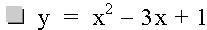
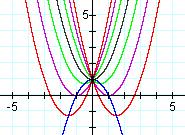
Graph of Quadratic Functions with varying values of b

 

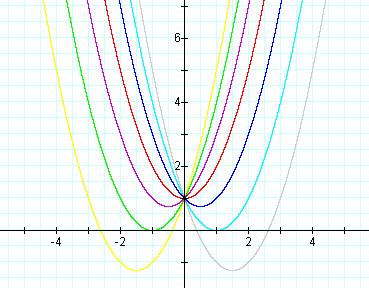
Let's now observe the graphs above:

The parabolas all pass through (0, 1). For b = -2, the parabola is tangent to the x-axis, so there is only one positive root. For b < -2, the parabola will intersect the x axis twice and both of the roots are positive real numbers. When b = 2, the parabola is tangent to the x axis, so again there is only one root, but this time negative. Finally, when b>2, there are two intersection points which are negative real numbers.

Looking closely at all of these quadratic functions, and marking the vertices it looks like there is a locus of points at y = -x² + 1

As we know, a proof is not in a graph. We know that the vertices of the quadratic function y = x² + bx +1 are the points where dy/dx = 0. The derivative is 2x+b so we can set that = 0, or:

2x + b = 0

b = -2x

Now we can substitute -2x into our equation for b:

y = x² + (-2x)x + 1 = -x² + 1

The vertices of the parabola indeed form the locus of points on y = - x² + 1.

 

Note this applies to a general quadratic equation, but the vertices are the points where:

dy/dx = 0 = 2ax + b.

thus b = -2ax