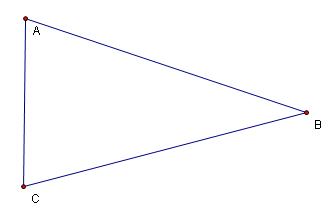
Step 1: Construct a triangle ABC

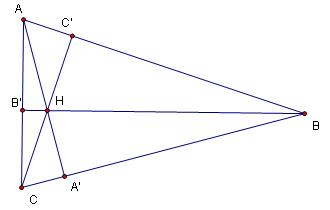
Step 2: Construct the three altitudes of an triangle ABC.
[Remember: an altitude of a triangle is a line segmet from the vertex of the triangle to the perpendicular foot of the opposite side (here A', B', and C').]
The three altitudes concur at the orthocenter. Let's refer to the orthocenter as "H".

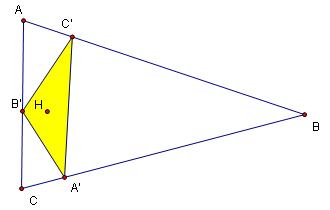
Step 3: Connect points A', B', and C' to make another triangle, which is the orthic triangle of triangle ABC.

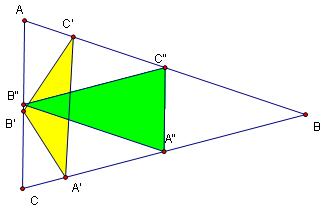
Step 4: Find the midpoints of the sides of the original triangle A", B", and C" and connect them to make another triangle, which is the medial triangle of ABC.

Step 5: Construct the midpoints from the orthocenter to each vertex and label them M1, M2, and M3.

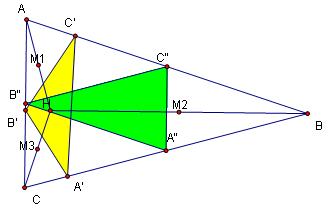
Step 6: Connect these three points, M1, M2, and M3, to form a third triangle -- which is called the image triangle (or the orthocenter midsegment triangle) of ABC.

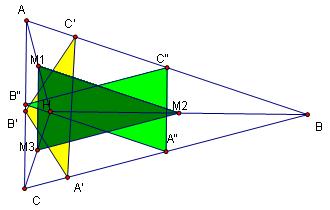
Step 7: Now we can connect nine points -- M1, M2, M3, A', B', C', A", B", and C" -- to form the nine-point circle.

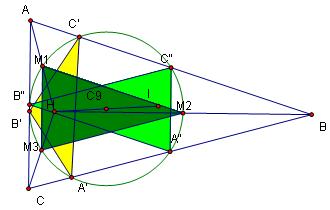
Note: The center of the nine-point circle, C9, is the midpoint between the orthocenter H and the incenter I.
[Remember, the incenter is the point of concurrency of the perpendicular bisectors of each side of the triangle.]

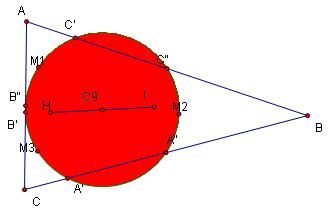
Key:
H = Orthocenter
I = Incenter
C9 = Center of Nine-Point Circle
A, B, and C are vertices of the original triangle
A', B', and C' are the triangles altitudes
A", B", and C" are the midpoints of the triangle sides
M1, M2, and M3 are the midpoints between the orthocenters and the three vertices of the triangle.