Assignment 6
Problem #6
by Margaret Trandel
I chose to explore the following problem using GSP:
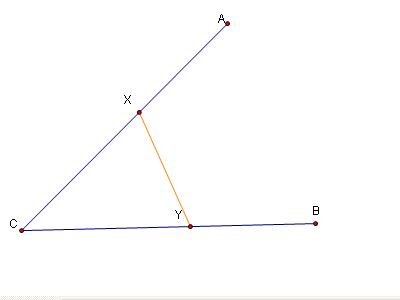
Given three points A, B, and C, draw a line intersecting AC in the point X and BC in the point Y such that:
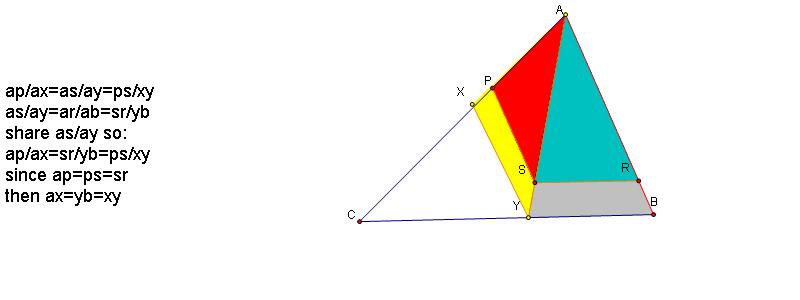
AX = XY = YB
Let's first look at a visual representing what we are trying to prove:
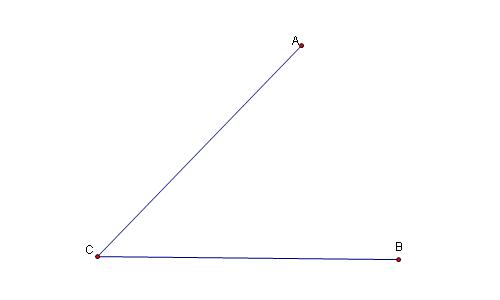
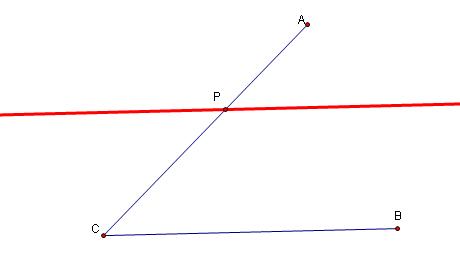
1. To develop a proof for arbitrary points A, B, C, X, and Y, let's start by constructing an arbitrary angle ACB.
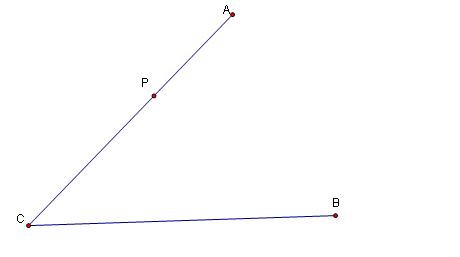
3. Now construct a random point on segment AC and call it P.
4. Construct a line which is parallel to BC and also passes through point P.
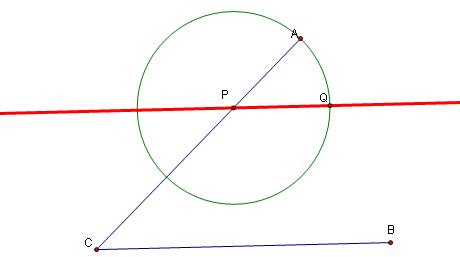
5. Now let's make a circle. The center should be at P and it should pass through point A.
6. Let's now construct a circle with center at Q and radius PQ.
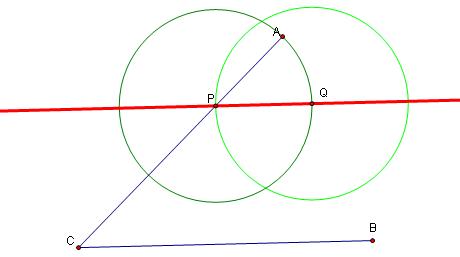
7. Connect points A and B and construct a line parallel to AB thru P . Note by AAA similarity theorem, triangles APQ and triangles ACB are similar.
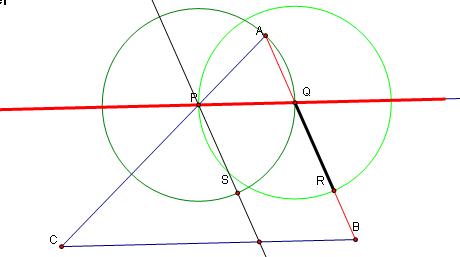
8.Connect S and R. Note the parallelogram PQRS. PS, PQ, QR and SR are congruent segments.
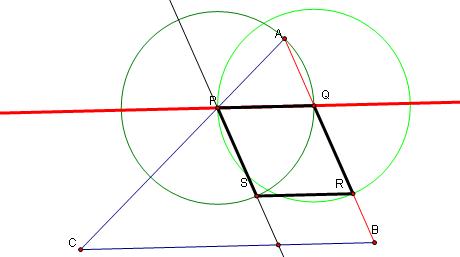
9.Draw a line connecting A and S. Label the point on line CB as Y.
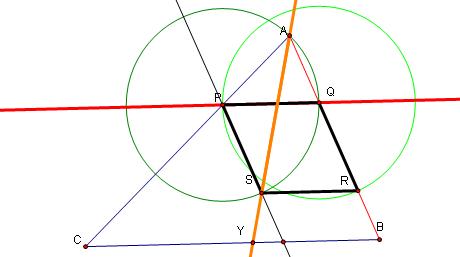
10. Construct a circle using YB as the Radius and A as the center. Label the point where the circle intersects side
AC of the triangle X. Note that Triangle APS and AXY are similar, as our Triangles ASR and AYB.
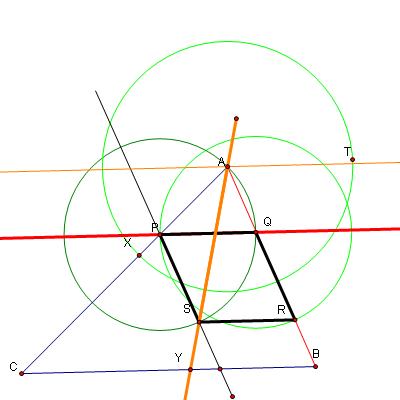
11. Now if all goes well, the measurements will eliminate all of the auxilliary lines and use the measurement tool to show that AX = XY=YB.
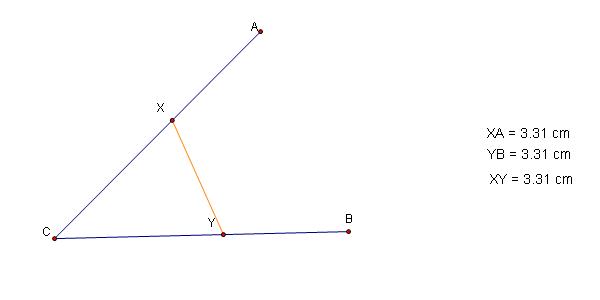
The construction circles and lines are eliminated on the sketch below to emphasize the equivalent ratios and substitution leading to AX=YB=XY