Assignment 8

Altitudes and Orthocenters

by Margaret Trandel

1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC. Note any observations, conjectures or proofs.

 

1. Construct a Triangle ABC

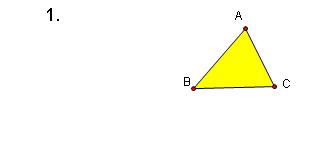
2. .Construct the Orthocenter, H of Triangle ABC. The Orthocenter is the intersection point of the three Altitudes.

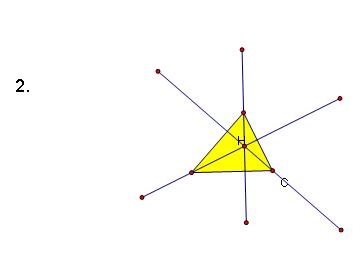
3. Construct the Orthocenter, H' of Triangle HBC

 

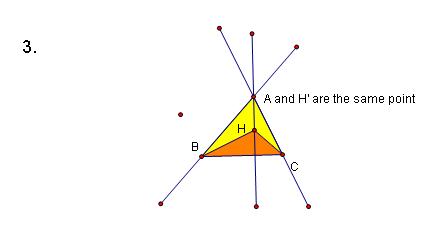
4. Construct the Orthocenter, H" of Triangle HAB.

 

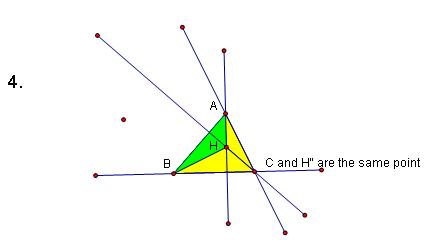
5. Construct the Orthocenter of Triangle HAC

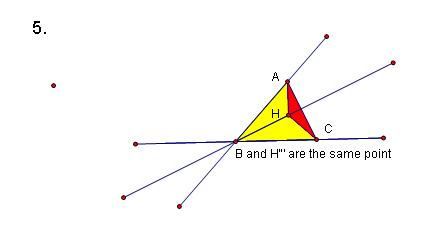
Now let's construct the circumcircles for each of the four triangles and explore any potential relationships. Recall that a circumcircle is the circle that passes through each of the three points of a triangle. To construct the circumcircle we find the concurrency point (incenter)of the perpendicular bisectors of the three sides and make that our circumcenter. Then we use any of the three vertices to determine the radius. I have left the incenter points for each circumcircle as well as the midpoints of each side. The auxillary lines are hidden. Also, for this investigation, let's enlarge the triangles in order to more easily make observations and/or conjectures.

6.Construct the Circumcircles of the following Triangles: ABC, HBC, HAB and HAC.

 

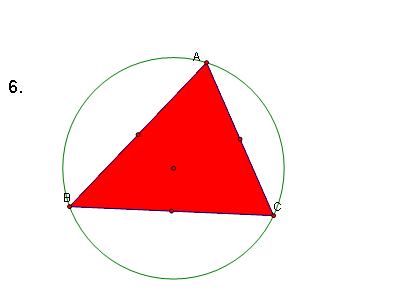
Circumcircle for Triangle ABC

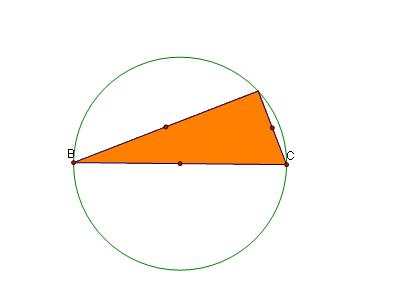
Circumcenter for Triangle HBC

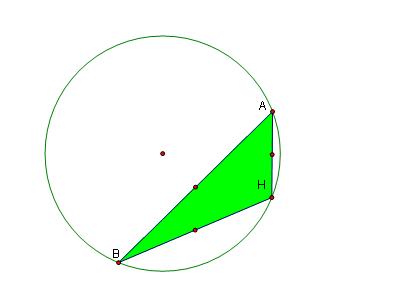
Circumcircle for Triangle HAB

Circumcenter for Triangle HAC

 

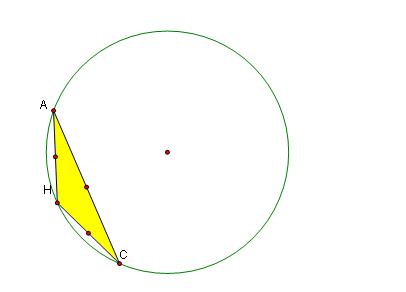
Now let's look at one single representation found in this gsp file of four triangles and their circumcircles. Open the gsp file to see one single representation. (You need the GSP program on your computer to open the file.)

My observations include the following:

The Circumcircles of the four triangles are congruent, since the radii are congruent.

The intersection of any two of the circumcircles of belonging to HBC, HAB or HAC is a vertex of the initial triangle, ABC

The orthocenter of : Triangle HAB is C, Triangle AHC is A and Triangle HBC is B. (see initial constructions)

The triangle formed by connecting the centers of the circumcircles for HAC, HAB, and HBC is congruent to the original triangle ABC.

All circumcircles pass through the orthocenter of ABC.