

Here we are looking at different pairs of linear functions. These functions are manipulated by addition, multiplication, division, and composites. We will look at 3 pairs of linear functions in this write-up.
![]()
![]()
And h(x) will be combinations of the above two linear functions.
![]()
First, let's look at h(x)=f(x)+g(x). Both functions are lines so the addition of these two functions should also be a line.
We see this can be simplified in to the equation h(x)= -1x - 6. This is an equation of a line like we said it should be. Let's graph it and see.
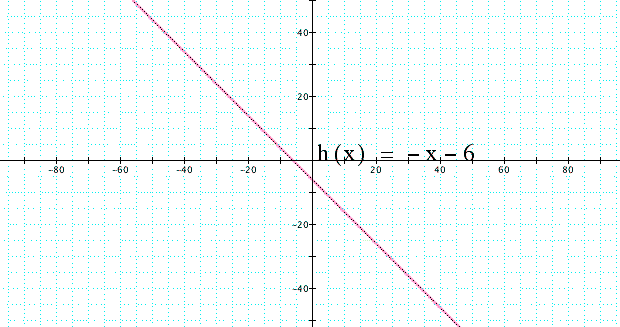
We see this graph is a line so we can conclude that the addition of two linear functions will give another linear function as a result.
Next, we will take a look at when h(x)=f(x)g(x).
The graph of this function becomes a parabola. Since the two degree one polynomials multiplied together give a degree two polynomial. Below is a graph of f(x) in purple, g(x) in red, and h(x) in black.
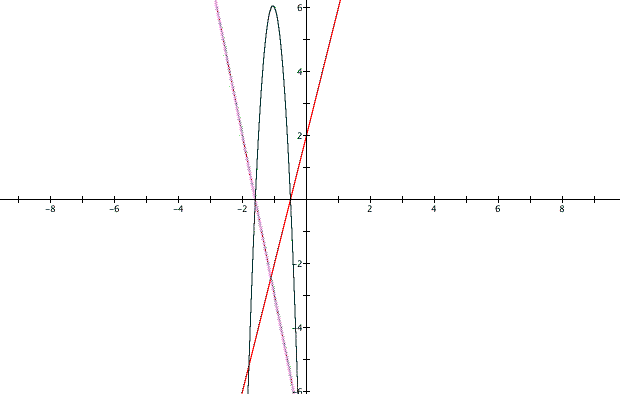
We see from the graph above that the two functions f(x) and g(x) are linear, but g(x) is not. It is a parabola. When we multiply the two functions f(x) and g(x) out we get:
![]()
We can see now that this is a quadratic function, therefore it makes sense that the product of two degree one polynomials is a degree two polynomial.
Now, lets take a look at what the graph of f(x) divided by g(x). So, we get h(x) to be:
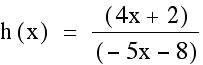
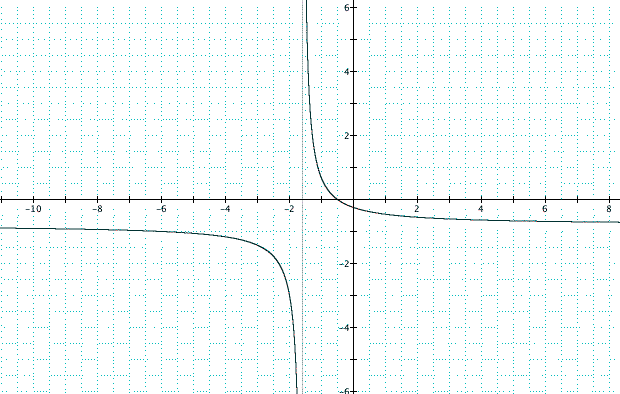
What do we think this graph is going to look at? Well, lets consider that we are dividing a degree one polynomial by another degree one polynomial. Since we are dividing, we cannot have a zero in the denominator so there are going to be some values that the function cannot take on. It appears to me that x cannot be equal to -8/5 since -5(-8/5)-8=0. This is an example of a value the function can never be. So let's take a gander at the graph and see what we notice.
The final h(x) we'll look at is a composition of f(g(x)). With compositions the x-value is plugged into the first equation, which here is g(x) and then the outcome of that equation is plugged into the second equation, which is f(x).
![]()
![]()
This time we are using different equations for f(x) and g(x). Thus the composition will be:
![]()
Now, by just looking at the equation we should be able to notice that the graph of h(x) should appear linear because we are not changing the degree of the polynomials at all. So let's look at this graph:
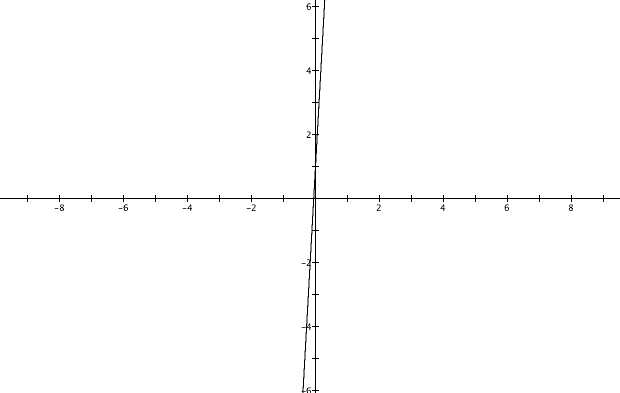
Our assumption that this graph was going to be linear was right. Manipulation of different linear functions will give different functions then the original.