

Here is the problem: We have a piece of cardboard that has the dimensions of 5 inches wide by 8 inches long. The problem is that we want to make a box without a lid made from squares cut out of each corner of the piece of cardboard that has the maximum possible volume. How do we do this?
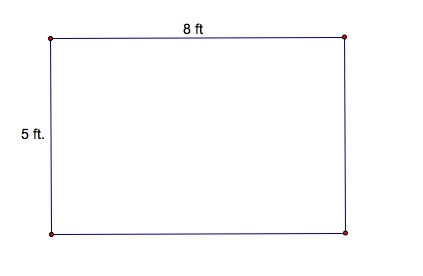
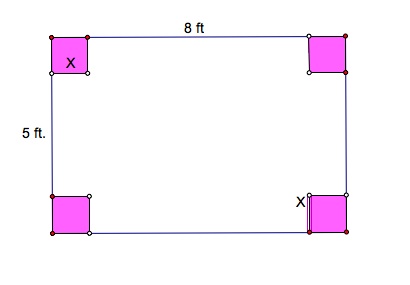
Here is our piece of cardboard. We will cut square pieces out of each corner of length x. So it should look like this:
Since we know the formula for the volume of
the box we can calculate this. ![]()
The length will be x, the height is 8-2x and the width is 5-2x.
We have to consider now that if x is larger than 2.5 the volume will be zero or negative which is not possible.
In excel I put in values for x from 0-2.5 and calculated the volume equation to get the volumes. After graphing I got a parabola even though it is a cubic function. This is because my domain is truncated.
Check it out here EXCEL
Now from this parabola we can see that the max volume is reached at one. The maximum volume at that point will be 18. Using our algebra and excel we were able to graphically see why this is. Funny how algebra creeps up into real-life situations like this.