This assignment takes a look at second degree functions. We will take a look at graphs in the form of
I will show the graph of this equation with different values substituted for a on the same axis. Before we see the graphs, let's think of some possible values for a.
a=1
a=-3
a=1/2
Now we have for different possible values for a. We see a can be positive, negative, rational, or irrational. How do you think these different values for a change the graph.
If the value is positive the parabola will open upwards, and if negative it will open downwards. The larger the value of a, the narrower the parabola will get. Once a is less than 1, the parabola will get wider and wider as the fraction gets smaller and smaller. Now what do we think will happen when a is irrational? It should have the same properties as if it were an integer or rational number, so let's finally take a look.
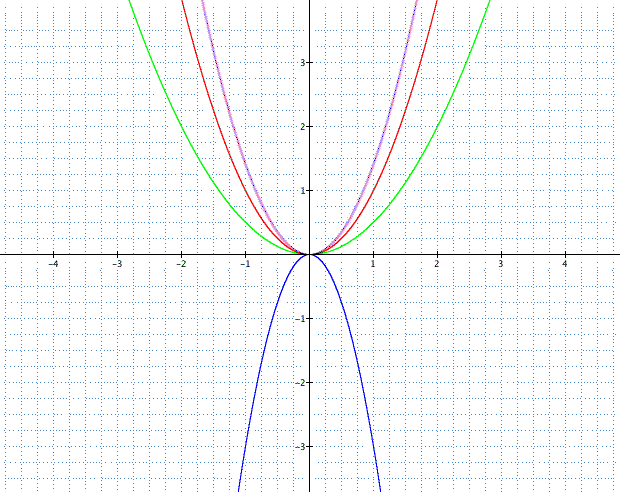
Purple=square root of 2
red=1
green=1/2
blue=-3
Is the trend I described above noticable in the graph above?
Well, the red curve has a=1 and the green curve is wider than the red and its a=1/2. This is expected from what I mentioned above. Look at the blue curve, it's flipped downward compared to the other curves and it is also narrower than the red curve because 3 is bigger than 1. Now what about the purple curve? The square root of 2 is larger than 1, therefore it will be narrower than the red curve even though it is only larger by a fraction.
It is evident that since the function
is just then the vertex will stay at the
origin and will not be shifted in any direction. The only thing
being changed in this equation is the coefficient in front of
the x squared. With four examples, it has been demonstrated what
happens to these graphs as the coefficient is changed by these
values. It is seen how the parabola gets narrower as the coefficient
becomes closer to zero, the parabola get narrower the further
away the coefficient is from one, and the sign infront of the
coefficient flips the parabola over the x-axis.