I'm going to have my students look at the relationship of lengths of the circumcenter and orthocenter to vertices of the triangle.
Given and arbitrary triangle ABC
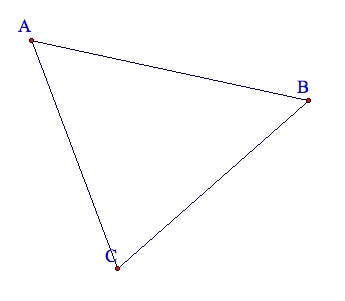
We are going to draw the circumcenter S, and the orthocenter O, and make a point M the midpoint of BC.
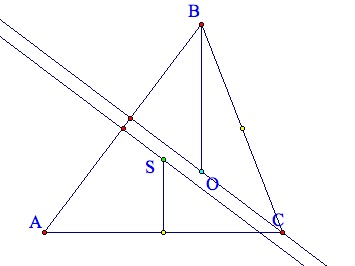
I rotated the triangle so we can use the coordinate system to show that SM = 1/2 BO. The point A is at the origin (0,0). The point C is at (c,0) and point B is at (a,b). Now let's look at S and O. The line going through S and intersects AB at the midpoint so that point is (a/2,b/2) in the coordinate system and M (the midpoint of AC) has the coordinates (c/2,0). We know the slope of line AB is b/a by definition of slope, thus the slopes of lines CO and S are -a/b by definition of perpendicular. So we get
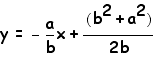for the line through
S and 
for the line CO.
We can use these equations to calculate the points of S and O.
S=(c/2,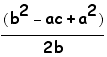 
) and
O=(a,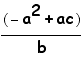 
)
Now the last thing we need to do is calculate the distances from S to M and B to O.
d(O,B)=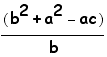 
d(S,M)=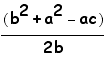 
Now we can compare the two differences to see if we proved that SM=1/2(BO). By just looking at the fractions we can see that d(S,M) is the same equation as d(O,B) except for a 2 in the denominator. Therefore we have proved that SM=1/2(BO).