

We are looking at two circles one inside the other. A line is drawn through the center of the larger circle.
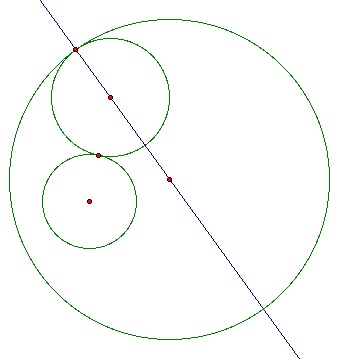
Now we need to construct the circle that is tangent to both the large and small circle in our picture. We get this circle to look like:
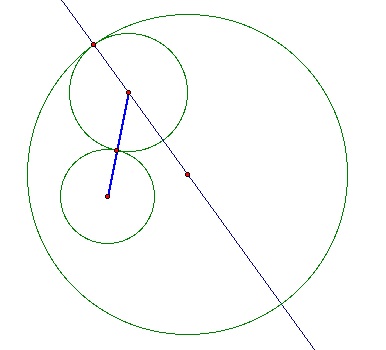
If we construct a line segment from the center of the small circle to the center of the desired circle we get something that looks like this:
This new segment has the length of the two radii ( the small circle plus the desired circle ). We can next construct an isoceles triangle by placing a copy of the small circle with its center at the point of tangency of the big circle and the desired circle.
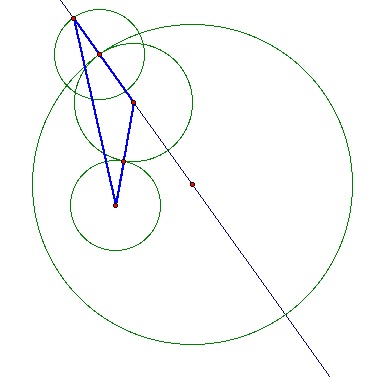
The locus of the center of the desired circle is going to look like an ellipse with the foci being the center of the two given circles. This ellipse can be seen here:

Through this investigation it is clear to me that a tangent circle can be constructed to two given circles in this fashion. As mentioned in the investigation the segment from the smaller circle to the desired circle will always be the sum of the two radii. Its interesting how two circles that are not intersecting or tangent to each other already can have another circle that connects them by tangency. The construction of the tangent circle takes basic knowledge of circles and segments, which is fasinating in the sense that young children should be able to do the construction of this as long as they have the knowledge of tangency.