

Earlier we found that the orthocenter is formed by constructing the three altitudes of a triangle and it is where they intersect. Now we're going to take a little bit deeper look at orthocenters.
First, draw an acute triangle, find the orthocenter and the circumcircle of the triangle.
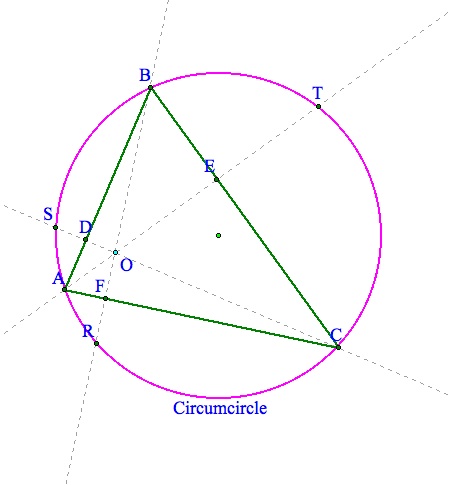
Now extend the altitudes of the triangle and label these intersections with the circle.
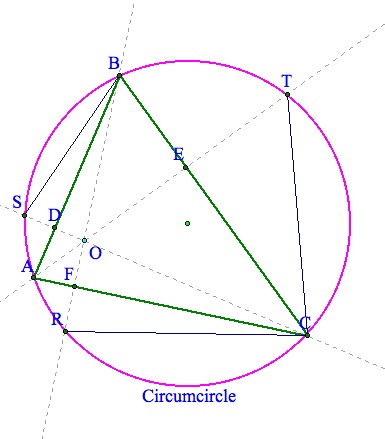
A ratio is now formed by the length of the altitude and the segment of the altitude plus the extension to the circumcircle.
It seems that after calculations that this sum of ratios equals 4
We can rewrite the top lengths to get:
So we can now write these ratios as:
Now we can see if this is true.
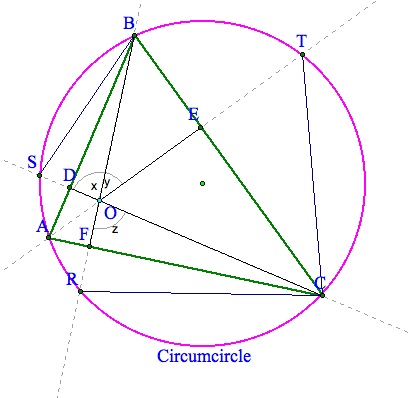
Now we can see with labels that since angle BEO is a right angle than angle EBO is 90-y. The same goes for angle BDO is right thus angle DBO is 90-x. And lastly since angle CFO is right then OCF is 90-z.
From this we can see that angle CBA=a=90-y+90-x. Then a+x+y=180 from this equation.
From the notion that if any angle on the circle shares a chord with another angle on the chord then these angle must be congruent, we can see that angle CBA=angle ATC=a.
From the picture we can tell that x=z because of vertical angles and therefore x+y+z=180 since they form a straight line. So we can combine equations to get a+x+y=x+y+z, so a=z=x.
We can see then that angle ETC=a=x=z. So then we have similar triangles.
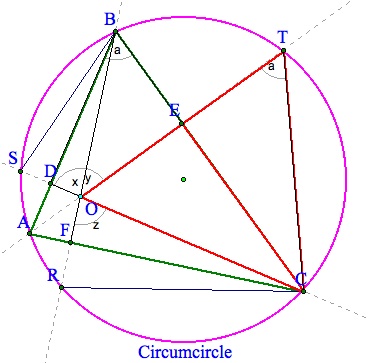
Since they share a side CE then not only are the triangles TEC and EOC similar they are congruent.
Thus ET=OE, the same can be said for OF=FR and DS=DO by repeating what we just did.
Let's look at that sum of ratios again with a little substitution.
Multiply ![]() by
by ![]() and we get:
and we get: ![]()
(OF)(AC) is actually 2 times the area of the triangle AOC. (BF)(AC) is actually 2 times the area of the triangle ABC. This can be similarly done with the other two ratios so that
So our sum simplifies to:![]()
Finally, we just proved what we wanted!