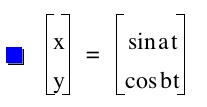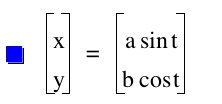Assignment Ten

 

Parametric Equations

Collaborative Effort by

Lucia Zapata and Claudette Tucker



 A parametric curve in the plane is a pair of functions

x=f(t)

y=f(t)

where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t and your work with parametric equations should pay close attention the range of t . In many applications, we think of x and y "varying with time t " or the angle of rotation that some line makes from an initial location.



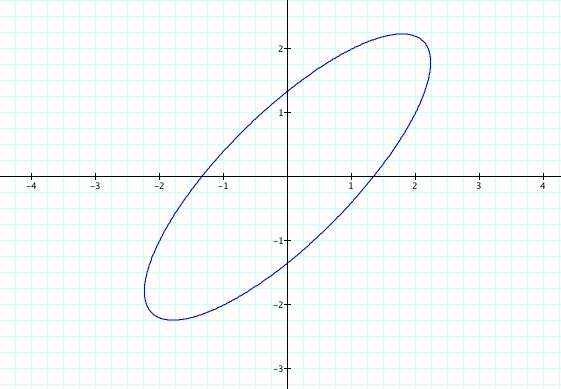
1. Let us compare what happen for the equations

x=cos(at)

y=sin(bt)

 

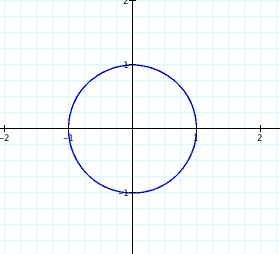
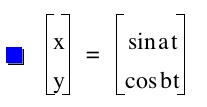If a=b, it does not matter always we can get a circle of radius 1. You can try here different values for a and b.

2. Let us explore now for the next equation

x=a cos(t)

y=b sin(t)

Could you guess what happen for different values of a and b?

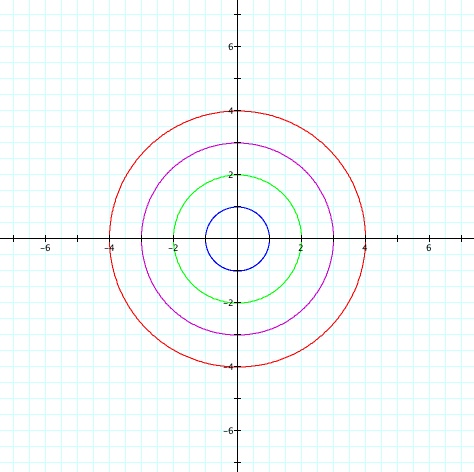
well, as you can see in the next graphic, if a=b we can get circles of different radius. The radius of those circles will depend on a=b. Try with different values for a and b here.

 

 

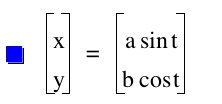Now try to think what about if a is different from b

You can explore with different values of a and b here. However, observe that a give us the intercept with x axis and b give us the intercept with y-axes. it looks like our initial circle were changing its form looking like an ellipse.

 

What is the curve when a < b? a = b? a > b?

What will happen if we combine the situation in 1 with the situation in 2? any idea?

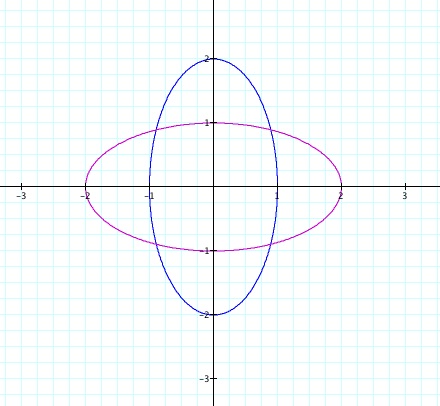
Let us try the next combined equations

x=a cos (t) + h sin (t)

y=b sin (t) + h cos (t)

If h=1 is easy to guess that the equations now depend on a and b, but we discovered previously that if a=b we get circles and if a<b or a>b we get ellipses. Observe that this time we have gotten an different ellipse.

You can try here different values of a, b and h and make your own conclusions

Return to my Homepage