

We will investigate a + bsin(ktheta) with different values of a, b and k.
If you graph r = a + bsin(ktheta) ,
how does it look? Before using your graphing calculator, can you
predict or make an educated guess on how it will look? Just give
it a try. Click here to see if
your prediction is correct.
Let's examine the polar equation above when a= 0, 1, 2, 3, 4, where b=1 and k=1
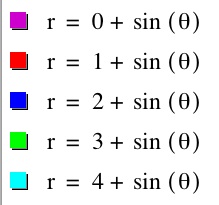
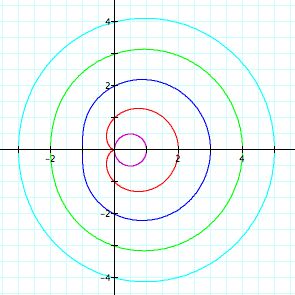
Conclusion: Compare these results to a + bcos(ktheta).
What are the differences and similarities? It still seems as though
that the values of a increases the graph slowly approaches the
form of a circle. We can conclude that the graphs are no longer
symmetric x-axis instead it is symmetric to the y-axis because
the position has been rotated ninety degrees counter-clockwise,
when compared to a + bcos(ktheta).
Let's examine the polar equation above when b= 0, 1, 2, 3, 4, where a=1 and k=1.
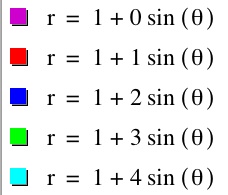
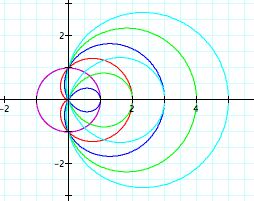
Conclusion: Again this graph has rotated ninety
degrees counter-clockwise, when compared to r = a + bcos(ktheta)
for b = 0, 1, 2, 3, 4, a = 1, and k =1. Is it symmetric to the
y-axis?
Since different values of a and b have both effected the equation, it is only fitting that we experiment with the values of k. Let k = 0, 1, 2, 3, 4, 5, 6, where a=1 and b=1.
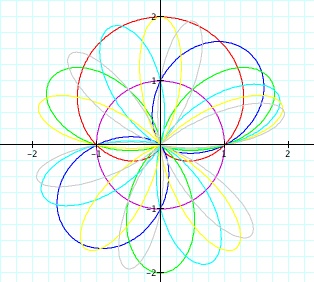

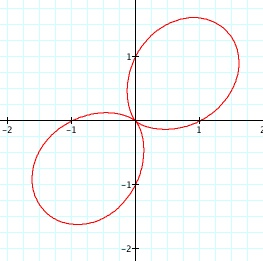
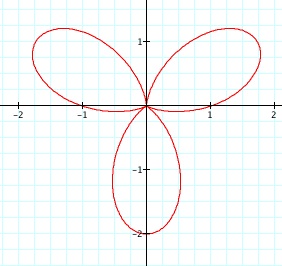
Conclusion: Looks interesting. Let's look at a couple of these separately, say k = 2, 3, 4,
| |
|
|
 |
 |
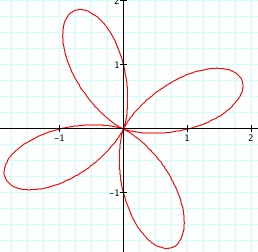 |
Conclusion: Click here to compare to r = a + bcos(ktheta) where k = 1, 2, 3, 4, b =1, a = 1. With this equation, it still seems as though that the value of k is a factor in determining the number of pedals that the rose contains or simply the n-leaf rose. There is a direct relationship to the value of k and n-leaf rose. Reflect on the chart above. When k = 2, 3 and 4 respectively, it creates a graph of a 2-leaf rose, 3-leaf rose, and 4-leaf rose. So n = k. Notice that the position of the graph is dissimilar to r = a + bcos(k theta) when k = 2, 3, 4.
How would you best describe this difference? Well, when k = 2, it seems as though the graph rotate forty-five degrees counter-clockwise. Determining the differences of k = 3 and k = 4 to r = a + b cos(k theta) also where k = 3 and k = 4 is quite a challenge.
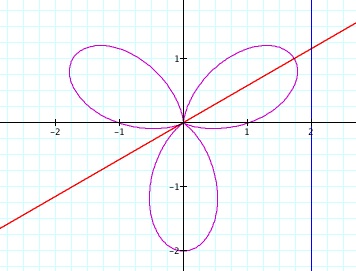
But through trial and error we decided to explore each graph separately with y = x and x=2 to see if there was any relationship between the tangent of rotations, the graphs, and slopes. When k = 3, we noticed that the degree of rotation is less than forty-five degree. If it did have a rotation of forty-five degrees, then the position of the leaf in the first quadrant would the same as the position of the leaf in first quadrant as k = 2. So this graph rotated somewhere between zeros to forty-five degrees. Let's assume that it's thirty degrees, which is the same as pi divided by four radians. Next, we found the tangent of thirty degrees, which is square root of three. The slope of the line will be 1 divided by the square of three. Let's check our conjecture by graphing our findings.
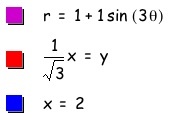 |
|
 |
 |
Therefore, r = 1+1sin(3theta) rotated thirty
degrees counter-clockwise. Can you determine how far r = 1 + 1sin(4theta)
rotated? Make an educated guess and then check your hypothesis.
What happens if cos(k theta) is replaced with tan(k theta)?
Click here to see what happens as n goes from O to 5.