
Assignment 11: Polar Equations
In this investigation I will explore the following three polar equations:
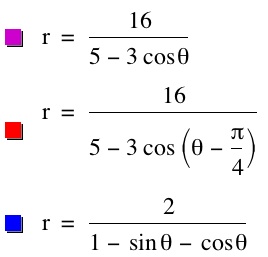
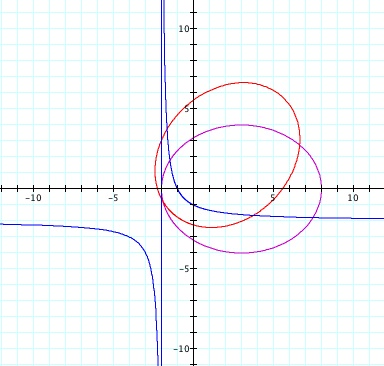
Polar equations are equations in terms of the polar coordinates, r and theta. r represents the distance a point is from the origin, and theta represents the angle the vector represented by a point makes with the positive x-axis. In our examples, the first two equations appear to be ellipses; the magenta ellipse appears to be an ellipse translated to the right from the origin, and the red ellipse appears to be the magenta ellipse rotated 45 degrees about the origin. The last equation appears to be for a hyperbola centered at (-2,-2) on the Cartesian plane.
First I will examine the magenta equation. Because I am not very familiar with polar coordinates, I will start by converting this back to a rectangular equation in terms of x and y. To do this I have to use the fact that the distance from the origin is the same as the square root of the sum of the squares of the x and y coordinates of a point. I also make use of the fact that cosine of theta is the same as the ratio of the x-coordinate to the distance from the origin. This follows from the familiar fact that cosine is the adjacent side over the hypotenuse.
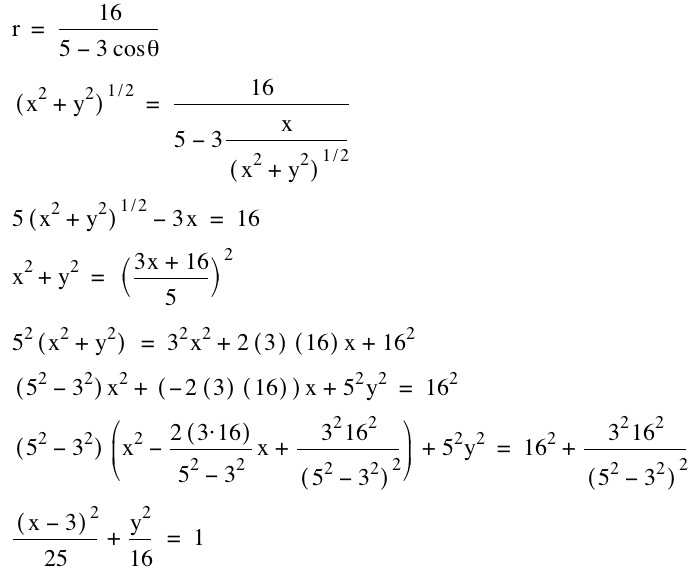
So the magenta equation does indeed represent an ellipse that has been tranlated 3 to the right from the origin. I can also see from this form of the equation that the greatest vertical height of the ellipse is 10 and the greatest horizontal width is 8. The three in front of the cosine of theta in the original equation is what gave the translation. Also, it seems like the reason the translation was in the x-direction is because cosine instead of sine was used. To check this hypothesis I will see if the same equation with a sine instead of cosine give the same ellipse translated 3 units up. In addition, I expect the lengths and widths to be reversed, since we will be completing the square in terms of y now.
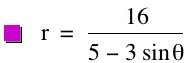
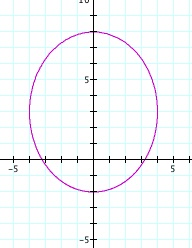
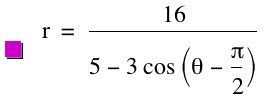
I was right! Now let's look at our original red equation. By observation, it seems that, just as subtracting a constant from x translates a graph left or right, adding an angle to theta rotates the graph by that angle about the origin. If this hypothesis is correct, then the equation graphed above should be the same as our original magenta equation after subtracting pi/2 from theta. This is because sine of theta is equal to cosine of the complement of theta. Indeed, the graphs are the same.
Next we must examine the last equation, the original blue equation. Again, I converted it to an equation in terms of the rectangular coordinates x and y.
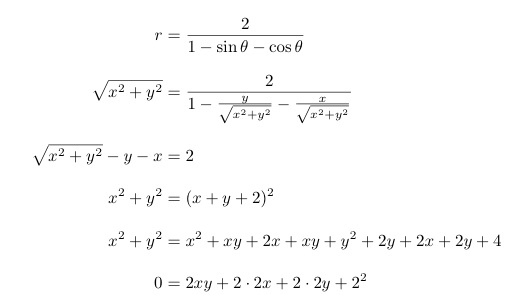
Now I can see that the xy terms will make this a hyperbola. Notice that the 2 in the numerator affects all x and y terms symmetrically, so that it would make sense for the hyperbola to be translated by the same amount in the x and y directions. In our example, the hyperbola was translated 2 to the left and 2 down. I hypothesize that if I change the numerator to any arbitrary number, the graph will translate that many units to the left and down. For example, if I change the numerator to -3, then the hyperbola will be centered at (3,3). Let's try.
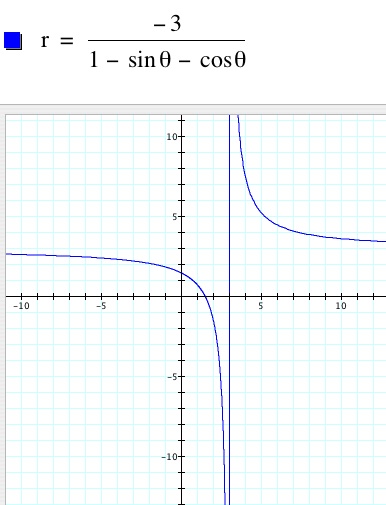
It worked! Now it's time to learn how to do Excel in Assignment 12.