

One of the investigations I did involving quadratic
equations was to look at solutions of ax^2+bx+c=0 on the xc-plane.
Below are some results of varying a and b independently of each
other.
First I varied the coefficient of x^2:
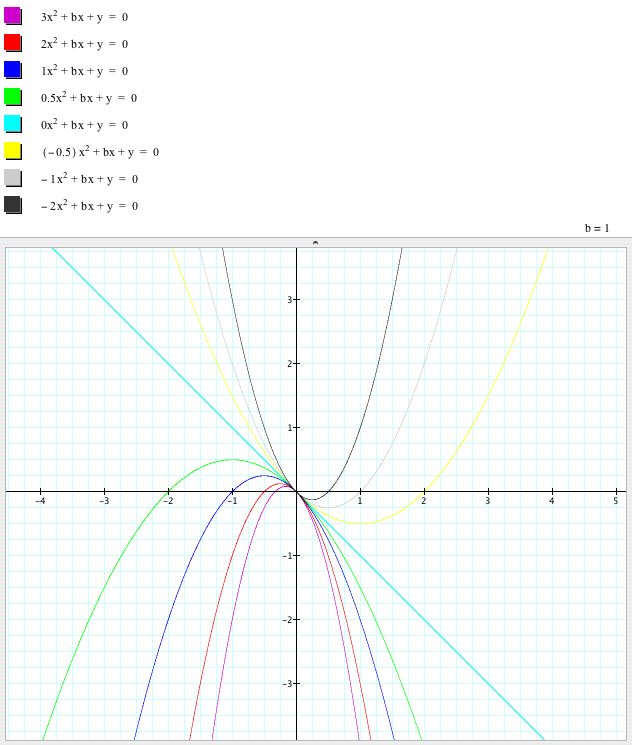
Then I varied the coefficient of x:
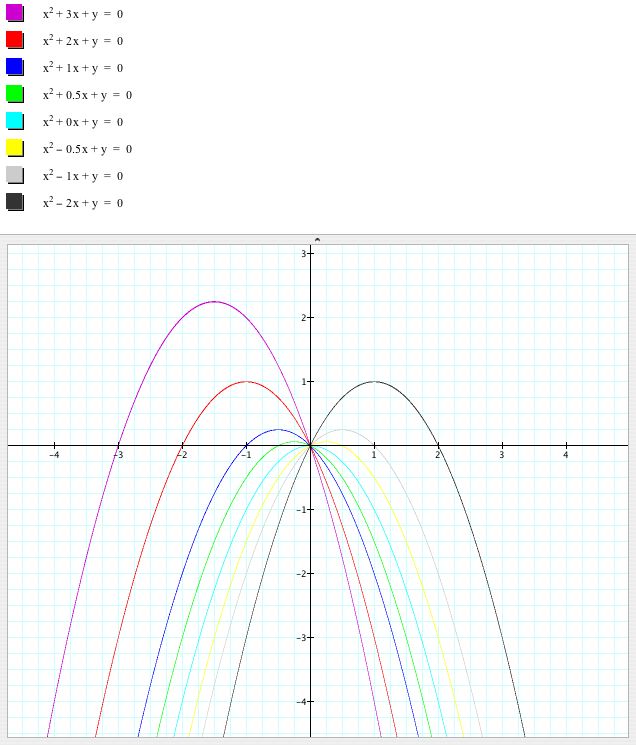
One salient feature was that the vertices of the parabolas formed when I varied b were points on another parabola. To figure out the equation of that parabola I noticed that the vertex of the parabola is (0,0) and another point on the parabola is (1,1). This led me to conjecture that the equation of the parabola formed by the vertices has the equation y=x^2. Below I have overlayed the graph of y=x^2 to see if it goes through each vertex:
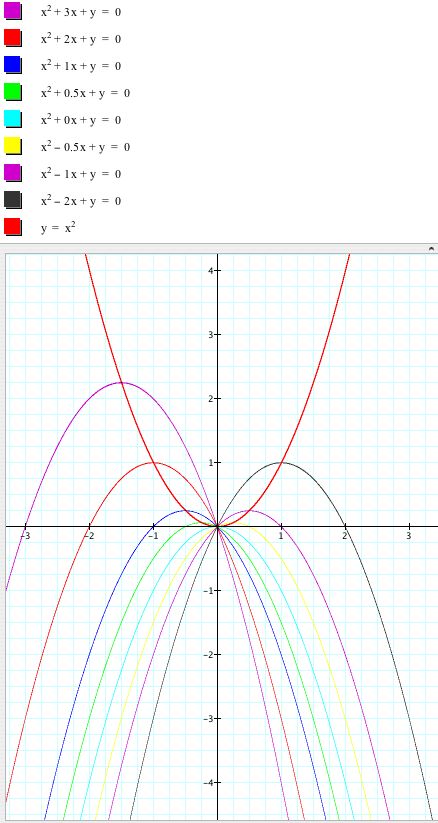
It seemed to be a good fit. The next question to ask myself was why the vertices formed this pattern.
If we start with our original equations, replacing the changing coefficient with a b, and then complete the square to get the equation of a parabola in standard form, we get:
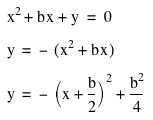
So each of the vertices of the parabolas will be of the form: (-b/2, b^2/4). In particular, the y-coordinate is always the square of the x-coordinate. Hence each of these vertices will be on the graph of y = x^2.