Every triangle has a special circle associated with it which passes through at most nine distinct points in the triangle: the midpoint of each side (labeled p1-p3), the foot of each of the three altitudes (labeled p4-p6), and the midpoint of each segment that connects a vertex to the orthocenter (labeled p7-p9).

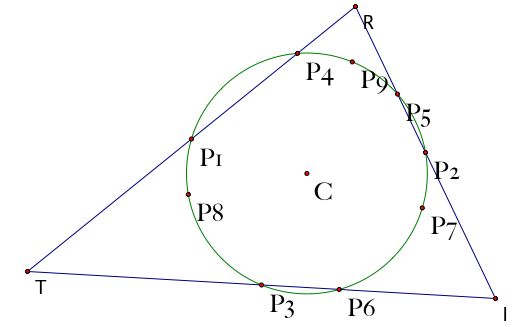
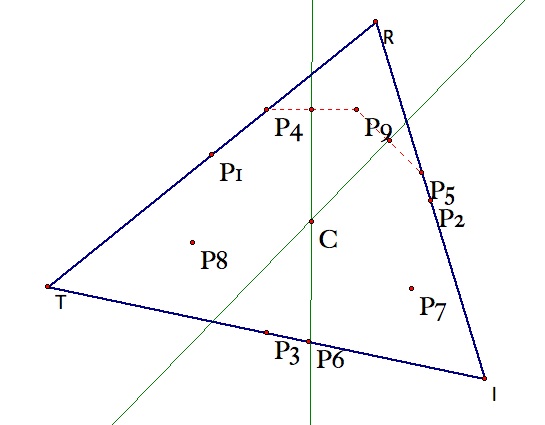
As long as you are comfortable with the constructions of midpoints and the orthocenter, the construction is fairly straightforward. One trick is finding the center. We know the perpendicular bisectors of chords always go through the center of the circle. So I found the center by constructing two chords of the nine-point circle (by connecting two pairs of points with line segments), and then finding the point of intersection of the perpendicular bisectors of the chords, as shown in the figure below.

[ If you would like to use a script tool in GSP that constructs a nine-point circle, open this link and go to the tools menu. Note: you must have GSP on your computer to use the link. ]

As I moved the vertices of the triangle around and watched the nine-point circle change, I started to wonder how many different numbers of distinct points are possible. For example, do the nine-points ever collapse to just eight points? Here are some of the facts I found:

• In an isosceles triangle the midpoint and the foot of the altitude coincide on the base, leaving eight distinct points.
• In an obtuse triangle one of the altitudes never intersects the opposite side, leaving at most seven distinct points.
• In an equilateral triangle there are six because the midpoints all coincide with a foot of an altitude. Also, in an obtuse isosceles triangle there are only six for reasons given above.
• In a right triangle there are at most five because the orthocenter is on the vertex of the right triangle, meaning that two of the sides are the segments connecting the orthocenter to the vertices. Hence two pairs of midpoints coincide.
• In an isosceles right triangle there are four. I know that there have to be at least three points, because the three midpoints of a triangle never coincide. Furthermore, the only way points 6, 7 and 8 (the midpoints of the segments connecting the orthocenter to the vertices), could coincide with any of the midpoints is if the orthocenter is on one of the vertices, in which case only two would coincide. Hence, we will always have at least four points.

Return to Katy's Home Page