

One of the basic constructions used when exploring tangent circles is how to construct the tangent line to a circle from a given point outside the circle. Below I will present two methods for doing this. In both you start with a circle and a point outside the circle.
Method 1: This method is more straightforward than the second method, but much more complicated. We know that in our finished product we can form a right triangle using the given point, the center of the circle and the point of tangency as the three vertices.
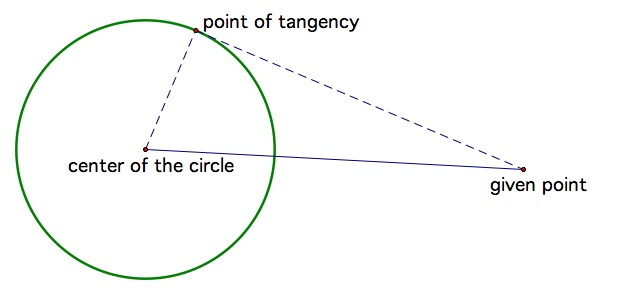
The only line we have to start with is the solid blue line above connecting the given point and the center of the circle. However, we can find the length of the radius easily enough, even if we do not know which radius exactly we will use for our triangle. So of the various parts of the triangle we can easily construct:
By HL, we should be able to construct a triangle congruent to the one we want.
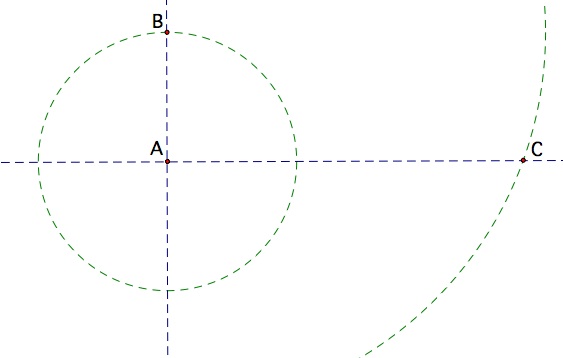
Start by constructing perpendicular lines, the dotted blue lines above, and find their intersection, A. Measure the radius of the circle and make a circle centered at A with the same radius. Now point B, where the circle intersects one of the original lines, marks the end of one leg of your right triangle. From there we will measure off the hypotenuse by making a circle centered at B and with a radius congruent to the length we had from our original figure. This circle will meet the other perpendicular line at point C, the final vertex of our right triangle. So AC has the length we were missing. Now, returning to our original figure we can make a circle centered at the given point and with a radius the length of AC, represented by the dotted arc in the figure below.
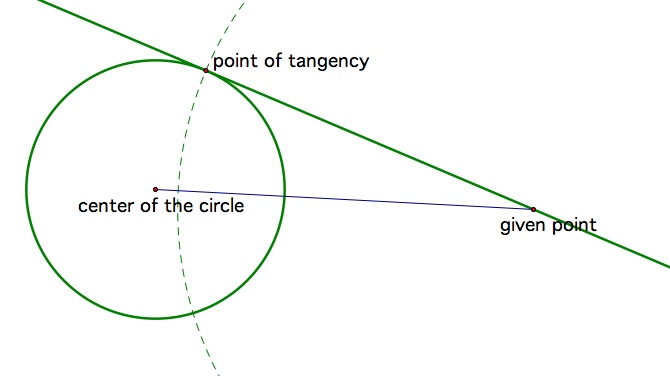
The point where this circle intersects our original circle is the desired point of tangency. And from there we can construct the line of tangency.
Method #2: In this method, we again consider the right triangle formed by the given point, the center of the circle and the point of tangency. All right triangles can be circumscribed in a circle with the hypotenuse as the diameter. But if the hypotenuse is the diameter, then the half the hypotenuse is the radius. So find the midpoint of the segment connecting center of the circle to the given point. Then construct a circle with the midpoint as the center and half the segment as the radius, the dotted circle below.
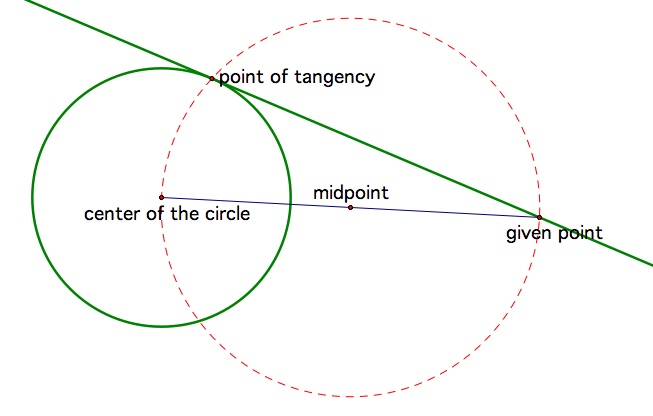
This circle should go through all three vertices,
so the point of intersection between the two circles will be the
point of tangency. From there we can construct the tangent line.
Teaching proofs is always a challenging part of geometry. Therefore I thought an interesting lesson arising out of the relationships between two circles and a tangent circle would start with the class constructing the following using GSP:
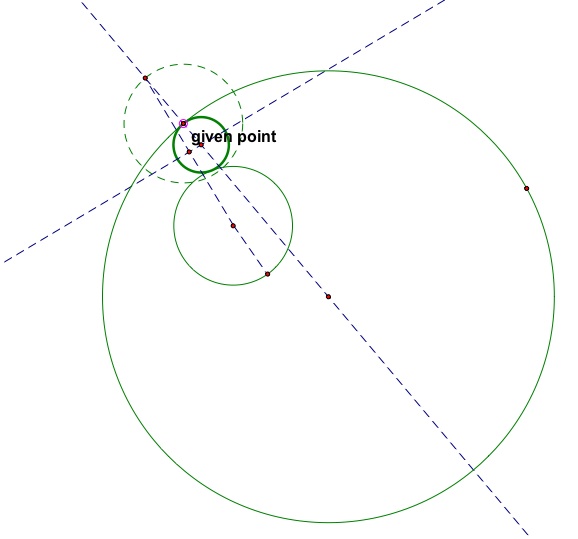
Basically, it is the construction of a tangent circle to two given circles given one point of tangency. Next I would have the students animate the given point of tangency while tracing the center of the tangent circle and tracing the perpendicular bisector of the segment connecting the two points of tangency in blue. The resulting shape from either trace appears to be an ellipse.
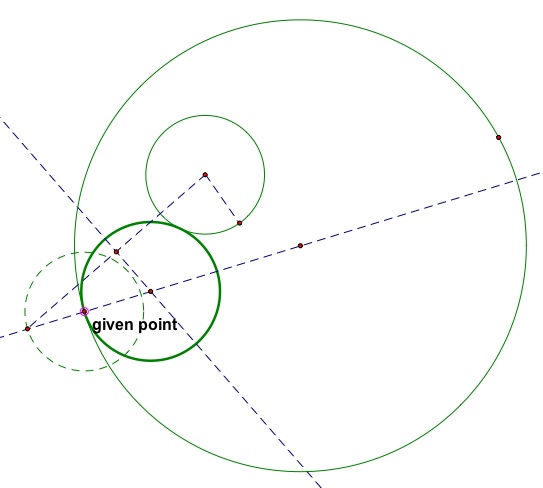
Then I would have the students prove that the resulting shape is an ellipse. Some questions that would help in thinking about the proof:
What is the locus definition of ellipse?
An ellipse is the set of all points for which the sum of the distances from two given points is a constant.
If our figure were an ellipse, what would that constant sum be?
The constant sum would be the sum of the radii of the two given circles.
We can see that the sum of distances is the sum of the radii at the two 'vertices' of our figure.
If our figure were an ellipse, what would the two foci be?
The vertices would be the centers of the two
given circles.
Now can we prove that the sum of the distances from two foci to
the center of our tangent circle is the sum of the radii of the
given circles?
Yes. Referring to the figure below, we constructed CD to be the
perpendicular bisector of BE. So BC = CE. The sum of the distances
from the two foci is AC + BC. By substitution,
AC + BC = AC + CE, which is the sum of the
two radii of the given circle.
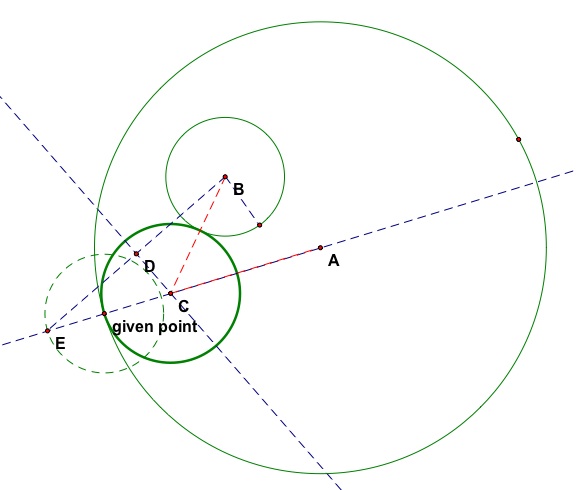
At this point, the students should be able to formalize the proof
individually.
Let us now consider the situation in which the two given circles delineate disjoint circular regions. The locus of centers of the tangent circle will always form a hyperbola. Below I have traced both the centers and the tangent line to the hyperbola to help make the result clearer.
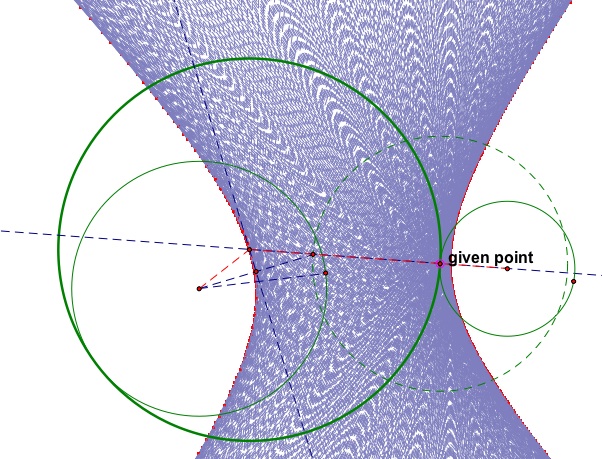
Note that in the above sketch one of the given circles is internally tangent to the tangent circle. If we make sure the tangent circle is externally tangent to both given circles, the locus of centers gives half of a hyperbola. The locus of the tangent lines outlines an entire hyperbola as is shown below:
