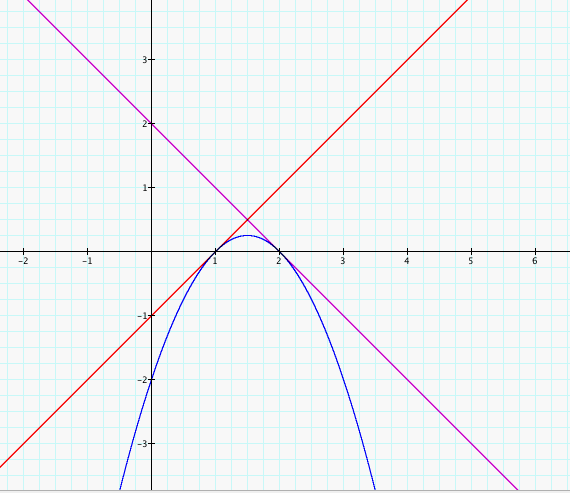
Problem
Describe two lines, f(x) and g(x) such that f and g are tangent to the product h(x) = f(x)g(x).

We have to get h(x)=f(x) *g(x).
We know for properties of product that h(x) will intersect with either f(x) or g(x) when either f(x) or g(x) are equal to zero. We can say that the intercepts of h(x) are the intercepts of f(x) and g(x)
We also know that h(x) must have to two real roots.

Let us to discover what are the characteristics of the slops and the intercepts of f(x) and g(x).

Let's start with the general case.

and their derivatives are

The roots of the lines are

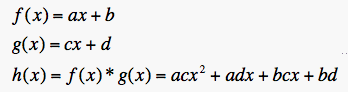
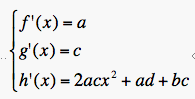
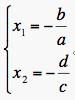
If we set the derivatives of f and h equal to each other at the first root, then we should find something about the constants a, b, c, and d.

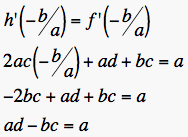(1)

Now let us do the same with the derivatives of g and h.

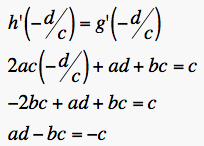(2)

From equations (1) and (2) sets and substitutions we get

a=-c (3)

This is very important information because now we know the characteristics of the slopes

Now lets to discover what happened with the intercepts. Let set the derivatives of f and h equal to each other at the first root, and substitute (3) to determine what happened with b and d

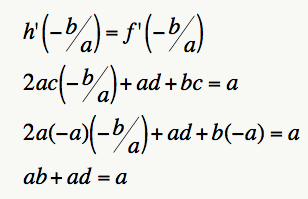
b+d=1(4)

So with (3) and (4) we have found the characteristics for slopes and intercepts of f(x) and g(x)

For instance f(x) = -x+2 and g(x)=x-1 satisfy the conditions

Return to my Homepage