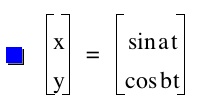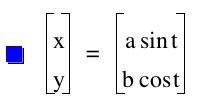Assignment Ten
Parametric Equations
Collaborative Effort by
Lucia Zapata and Claudette Tucker
A parametric curve in the plane is a pair of functions
x=f(t)
y=f(t)
where the two continuous functions define ordered
pairs (x,y). The two equations are usually called the parametric
equations of a curve. The extent of the curve will depend on the
range of t and your work with parametric equations should
pay close attention the range of t . In many applications,
we think of x and y "varying with time t
" or the angle of rotation that some line makes from
an initial location.
1. Let us compare what happen for the equations
x=cos(at)
y=sin(bt)
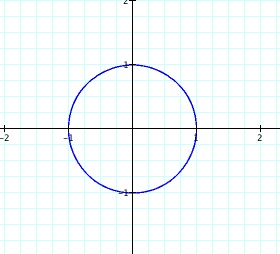
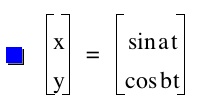 If a=b, it does not matter always we
can get a circle of radius 1. You can try here
different values for a and b.
If a=b, it does not matter always we
can get a circle of radius 1. You can try here
different values for a and b.
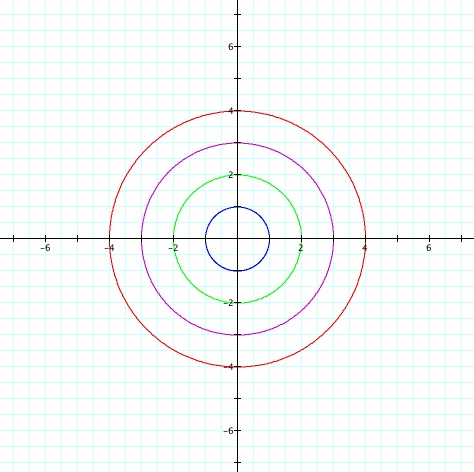
2. Let us explore now for the next
equation
x=a cos(t)
y=b sin(t)
Could you guess what happen for different
values of a and b?
well, as you can see in the next graphic,
if a=b we can get circles of different radius. The radius of those
circles will depend on a=b. Try with different values for a and
b here.
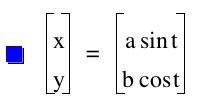 Now try to think what about if a is
different from b
Now try to think what about if a is
different from b
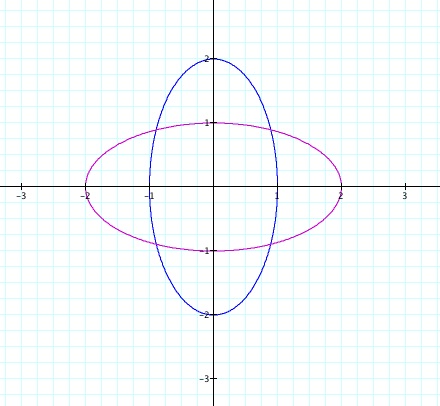
You can explore with different values of a
and b here. However, observe that a
give us the intercept with x axis and b give us the intercept
with y-axes. it looks like our initial circle were changing its
form looking like an ellipse.
What is the curve when a < b? a = b? a >
b?
What will happen if we combine the situation
in 1 with the situation in 2? any idea?
Let us try the next combined equations
x=a cos (t) + h sin (t)
y=b sin (t) + h cos (t)
If h=1 is easy to guess that the equations
now depend on a and b, but we discovered previously that if a=b
we get circles and if a<b or a>b we get ellipses. Observe
that this time we have gotten an different ellipse.
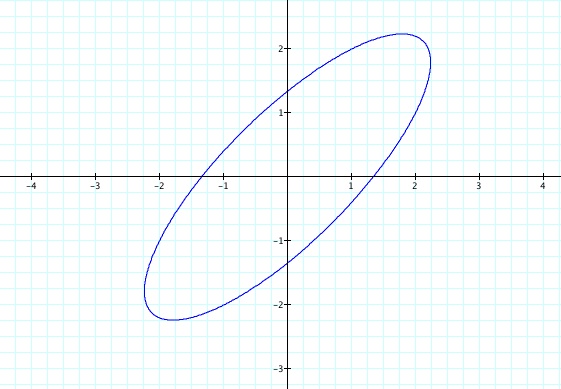 You can try here
different values of a, b and h and make your own conclusions
Return to my Homepage
You can try here
different values of a, b and h and make your own conclusions
Return to my Homepage