

1. Investigate r = a + bcos(ktheta). Note: When a andd b are equal, and k is an integer, this is one textbook version of the "n-leaf rose." Compare with r = bcos(ktheta) for various k.
What if ...cos ( ) is replaced with sin
( )?
If you graph r = a + bcos(ktheta) , how does it look? Before using your graphing calculator, can you predict or make an educated guess on how it will look? Just give it a try. Click here to see if you assumption is correct.
Let's examine the polar equation above when a= 0, 1, 2, 3, 4, where b=1 and k=1.
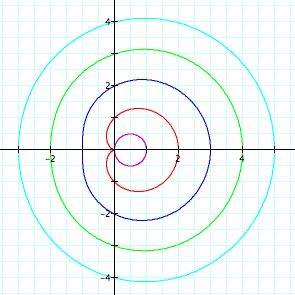
From the graph of different values of a, it seems as though that we can draw a conclusion. As the value of a increases, the graph begins to transform into a circle.
Let's examine the polar equation above when b= 0, 1, 2, 3, 4, where a=1 and k=1.
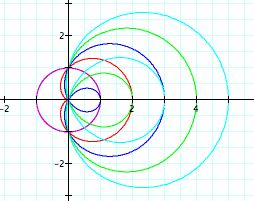
From the graph of different values of b, it
seems as though that we can draw another conclusion. As the values
of b increase, the loops expand and double for values of b greater
than one. Compare this graph to the one noted above. What other
conclusions can you draw? What are some differences in the two
graphs?
Since different values of a and b have both effected the equation, it is only fitting that we experiment with the values of k. Let k=0, 1, 2, 3, 4, 5, 6, where a=1 and b=1.

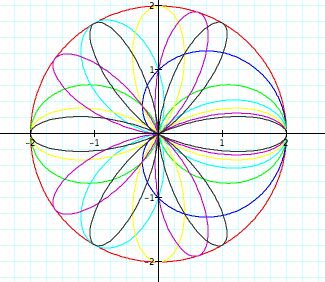
Oh, interesting! Do you see a pattern among the graphs? Pay close attention to the each individaul graph. K has an effect on the graph. Let's what happens see if we look at some the graphs individually.
|
|
|
|
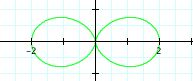 |
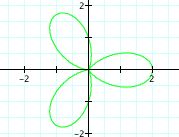 |
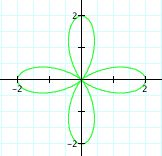 |
Even though we failed to explore how each value of k looked separately, we can gather something from observing the above equations at k = 2, 3, and 4. The value of k effects the number of leaves or pedals on the rose. When a =1, b =1, and k = n, where n = any integer, there will be a n-leaf rose .
Click here if you like to explore other values of k when
a and b are equal to one.
Click here to see the Exploration of r=bcos(ktheta).