

A guy walks into a 7-11 store and selects four
items to buy. The clerk at the counter informs the gentleman that
the total cost of the four items is $7.11. He was completely surprised
that the cost was the same as the name of the store. The clerk
informed the man that he simply multiplied the cost of each item
and arrived at the total. The customer calmly informed the clerk
that the items should be added and not multiplied. The clerk then
added the items together and informed the
customer that the total was still exactly $7.11.
What are the exact costs of each item?
Solution
We are able to set up two equations with the given information.
Where w, x, y and z are the prices of the four items.
Because we only have two equations and four unknown quantities, the system has multiple solutions.
One of the things I discovered before any calculation is that w, x, y and z have some restrictions. Their values must be between 0.7 and 3.2, if one item cost more than 3.2 the product will be bigger than 7.11. To have a clear picture of this statement explore with different values of see this situation.
Taking into account those restrictions we are able to assign any value for w between 0.7 and 3.2 and see what happen with the rest of the values.
Let assume that w=1. The following graphic illustrates the set of solution for w=1. The purple 3D-figure represents the product, and the red plane represents the addition of the four items. If you want to try different values by yourself click here.

Next table generates some solutions for the problem
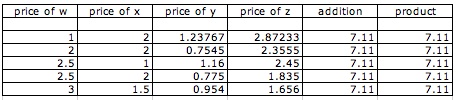
This is a subset of the set of infinitive solutions. However, those solutions are not very appropriate for our problem since it is very restricted. We have to find dollar with cents. It is still basically a problem with Diophantine Equations. Even though we have more variables that equations, there are restrictions on the variables.
In Diophantine Equations a usual restriction is that the values are all integers. Quite often the restriction to integers reduces the set of multiple solutions. If we make the following transformation to our problem, it could be solve as a Diophnatine Equation.
We have A + B + C + D = 7.11 and ABCD = 7.11.
If we think our problem as whole numbers it will be easier
Let x = 100A, y = 100B, z = 100C, w = 100D.
Then x + y + z + w = 711
xyzw = (100A)(100B)(100C)(100D) = 100000000(ABCD) =100000000(7.11) = 711000000
Now, our problem is reduced to solve a Diophantine Equation.
So, our problem will be a factorization of 711000000 in four numbers. Remember, we found above the numbers must be smaller than 3.70 dollars, that means that we have to find values smaller than 370. 711000000 can be expressed in its factors.
So we have to find the appropriate combination with the factors of 711000000.
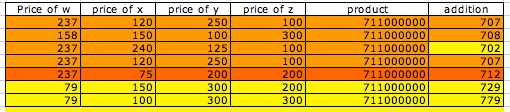
If you look at the column for addition you will note that some
values are really approximates but not exactly.