

Take an acute triangle ABC. Construct H and the segments HA, HB, and HC. Construct the midpoints of HA, HB, and HC. Connect the midpoints to form a triangle. Prove that this triangle is similar to triangle ABC and congruent to the medial triangle. Construct G, H, C, and I for this triangle. Compare
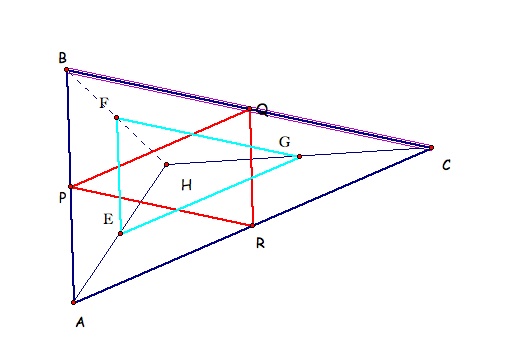
Before proving this statement let us to explore what is going on with the areas of the two triangles, the medial triangle and with the triangle constructed with the midpoints of the segment AH, CH and BH
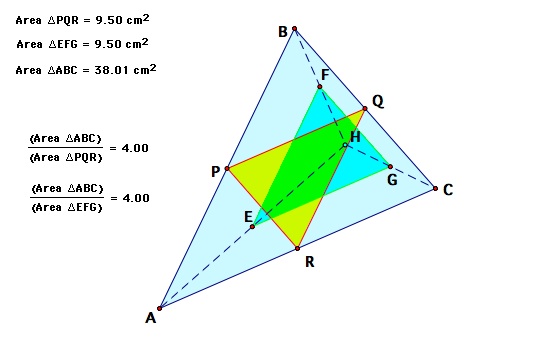
One interesting relation is the ratio between the areas try yourself with different triangles here.
But we can also compare with similar segments using the fact that the midpoints of the side of triangles generate parallel lines.
Let us prove that the new triangle EFG is similar to triangle ABC.
EG = 1/2 AC, EF = 1/2 AB, FG = 1/2 BC since E, F, and G are midpoints of HA, HB, and HC respectively.
EG/AC = EF/AB = FG/BC = 1/2.
Therefore, triangle EFG is similar to triangle ABC since the ratios of the corresponding sides are equal (1/2).
Now, let us prove that triangle EFG is congruent to the medial triangle PQR, of triangle ABC.
EG = 1/2 AC, and PQ=1/2 AC. Then EG = PQ
EF = 1/2 AB, and PR=1/2 AB. Then EF = PR
FG = 1/2 BC, and RQ=1/2 BC. Then FG = RQ