

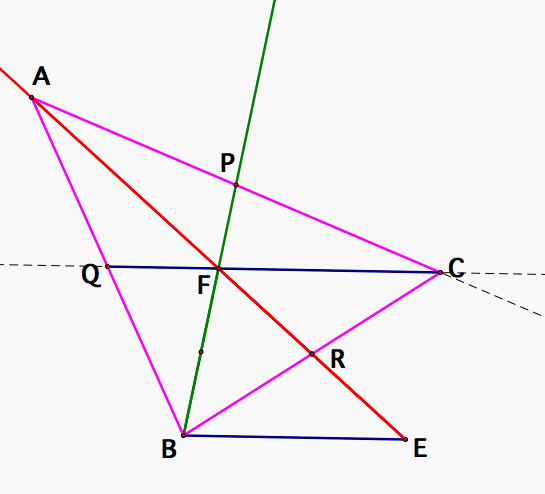
Given three line segments j, k and m. If these are the medians of a triangle, construct the triangle.
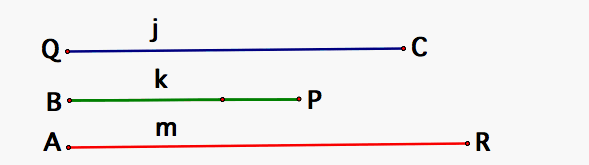
We now that the three medians of a triangle meet in a point at 2/3 from each vertex.
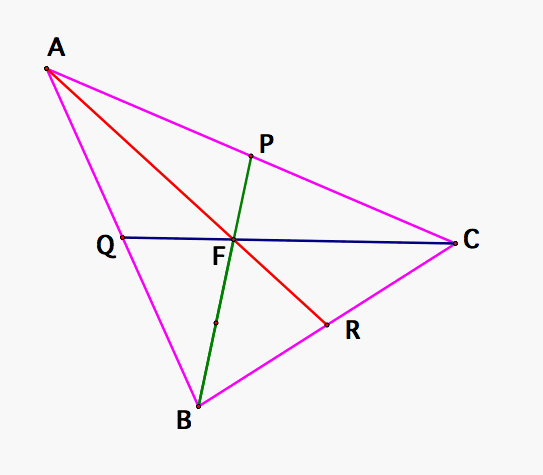
Now we need to take 2/3 of each median to construct a triangle.
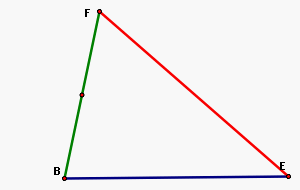
Next, prolong segment BF 1/2 times BF until P, prolong EF a length equal to EF until A. Through F trace a parallel to BE until that parallel meets the prolongation of AP
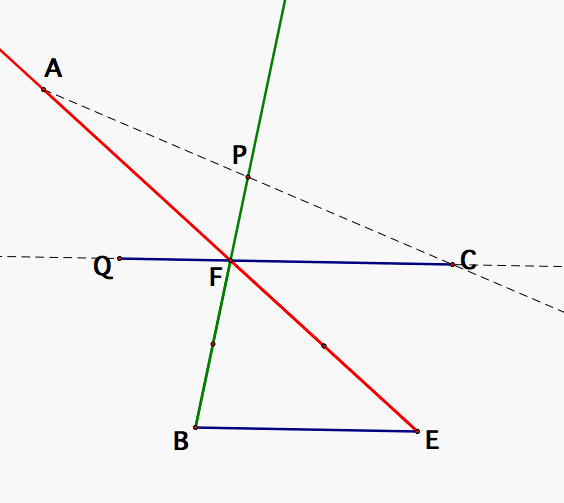
Now construct the segments AB, BC and CA. Now ABC is our triangle constructed with the three medians.
We can wonder what is the relationships
between the area of a triangle and the area of a triangle constructed
with its medians. You can explore here and
make some conjectures. We found that the areas of those triangles
have a ratio of 3/4.
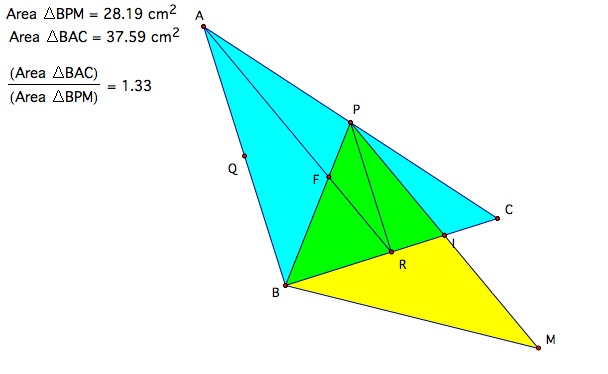
We can observe the following relationships between areas:
Therefore, area of BPI is 1/6+1/12+1/8 of ABC area. So, area of BPI is 3/4 of ABC area.