

McDonalds sell Chicken McNuggets in boxes of 6, 9, or 20. Obviously,
one could purchase exactly 15 McNuggets by buying a box of six
and a box of 9.
o Could you purchase exactly 17 McNuggets?
o How would you purchase exactly 53 McNuggets?
o What is the largest number for which it is impossible to purchase exactly that number of McNuggets?
o What if the McNuggets were available in boxes of 7, 11, and
17? What is the largest number for which it is impossible to purchase
that number of McNuggets?
This problem is very interesting since it introduces to modular arithmetic. To solve this problem we must do a rigorous and organized exploration to find the solution. Althought an algebraic solution can be use to solve this problem, the use of spreadsheet can provide an alternative view of the mathematics involved. This essay will show how spreadsheet can be used for explorations.
Solution
To answer the first question, it is impossible to purchase exactly 17 McNuggets. We would have to purchase 18 (three boxes of 6 or two boxes of 9) and have a McNugget left over.
For the second question, it is possible to purchase 53 McNuggets
by purchasing either:
o One box of 6, three boxes of 9, and one box of 20
o Four boxes of 6, one box of 9, and one box of 20
To answer the third and the fourth questions we require more
analysis.
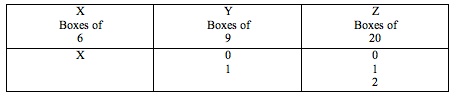
To begin notice that 2 boxes of 9 is the same of 3 boxes of 6.
Then let us to consider we are going to use either 0 or 1 boxes
of 9. With boxes of 20 we can change 3 boxes of 20 for 10 boxes
of 6. So, the amount of boxes of 20 we are going to use is ether
0. 1. or 2. And for the boxes of 6 we are going to use whatever
needed amount. Let us call X that amount.
We can establish our equation 6X+9Y+20Z=W
We can express W in terms of different combinations of X, Y and
Z which are 6 different combinations
(case 1) 6X+ 0Y +0Z = 6X + 0
(case 2) 6X+ 0Y +1(20) =
6X+ 0Y +1(3*6+2) = 6(X + 3)+2
(case 3) 6X+ 0Y +2(20) =
6X+ 0Y +2(3*6+2) = 6(X + 7)+4
(case 4) 6X+ 1(9) +0Z =
6X+ 1(6+3) +0Z = 6(X + 1)+3
(case 5) 6X+ 1(9) +1(20) =
6X+ 1(6+3) +1(6*3+2) = 6(X + 4)+5
(case 6) 6X+ 1(9) +2(20) =
6X+ 1(6+3) +2(6*3+2) = 6(X + 8)+1
In this part of the analysis, the introduction of thecnology will encourage students to do some explorations. As an example we can use our equation 6X+9Y+20Z=W to generate some values in a spreadsheet. Additionally, from table 1 we know that there are six different combinations between the values of Y and Z
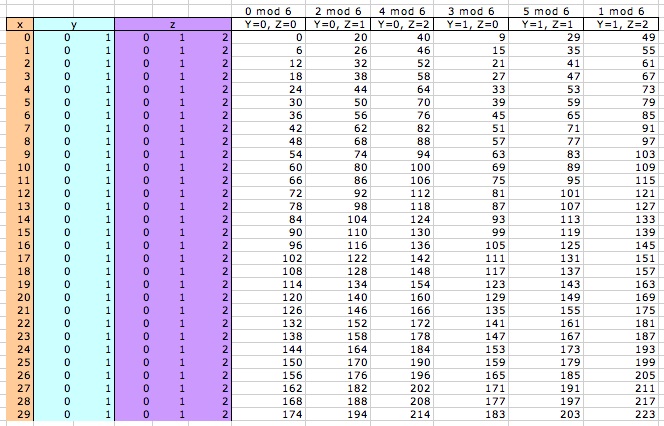
From the values in our combination we realize that every combination gives us a set of values that are congruent module 6. This means that all the values got from the column Y=0 and Z=0 are congruent module 6 because all of them have the same residual. Another interesting aspect is that the numbers generated in a column of the spreadsheet are not repeated in another column because every column has a different module.
Since we can get the residuals 0, 1, 2, 3, 4, and 5, we can express W in terms of factors of 6, 9 and 20 for big numbers of W. To answer the third and the fourth question we have to figure out which the big values are. I my analysis I have used modular arithmetic (where the residuals are called modules) and I built the next table
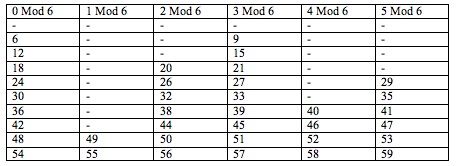
The empty cells mean that is not possible to buy exactly that amount of McNuggets using boxes of 6, 9 and 20
From the Table 3 we are able to answer the third question. The largest number for which is impossible to purchase exactly number of McNuggest is 43.
To answer the last question we will have to make a similar analysis, but in this case our module is 7.
To begin notice that 1 box of 11 and one box of 17 is the same of 4 boxes of 7. Then let us to consider we are going to use either 0, 1, 2, 3 or 4 boxes of 11, however not always we have to use boxes of 17. We only need boxes of 17 when we do not we boxes of 11. If we do not use boxes of 11, the amount of boxes of 17 we are going to use is either 0, 1 or 2. And for boxes of 7 we are going to use whatever amount we need. Let us call X that amount.
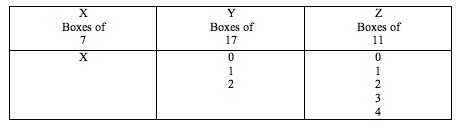
We can establish our equation 7X+17Y+11Z=W
We can express W in terms of different combinations of X, Y and
Z which are 7 different combinations. Notice that the combination
one box of 17 (Y=1) and one box of 11 (Z=1) is equals to 4 boxes
of 7. So we can eliminate that option to reduce our set of possibilities.
(case 1) 7X+ 0Y +0Z = 7X + 0
7X+ 0Y +0(11) = 7X + 0 (0 mod 7)
(case 2) 7X+ 0Y +1Z =
7X+ 0Y +1(11) =
7X+ 0Y +(7*1+4) = 7(X +1)+ 4 (4 mod 7)
(case 3) 7X+ 0Y +2Z =
7X+ 0Y +2(11) =
7X+ 0Y +(7*3+1) = 7(X + 3)+ 1 (1 mod 7)
(case 4) 7X+ 0Y +3Z =
7X+ 0Y +3(11) =
7X+ 0Y +(7*4+5) = 7(X + 4)+ 5 (5 mod 7)
(case 5) 7X+ 0Y +4Z =
7X+ 0Y +4(11) =
7X+ 0Y +(7*6+2) = 7(X + 6)+ 2 (2 mod 7)
(case 6) 7X+ 1Y +0Z =
7X+ 1(17) +0(11) =
7X+ (7*2+3) +0(11) = 7(X + 2)+ 3 (3 mod 7)
(case 7) 7X+ 2Y +0Z =
7X+ 2(17) +0(11) =
7X+ (7*4+6) +0(11) = 7(X + 4)+ 6 (6 mod 7)
As we did before, we can use spreadsheet to make some explortions in the pattern
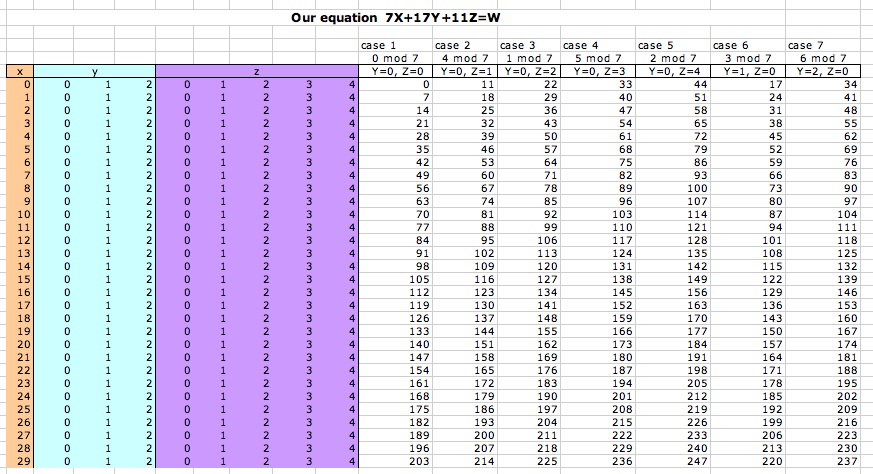
From the values in our combination we realize that every combination gives us a set of values that are congruent module 7. This means that all the values got from the column Y=0 and Z=0 are congruent module 7 because all of them have the same residual. Another interesting aspect is that the numbers generated in a column of the spreadsheet are not repeated in another column because every column has a different module.
Since we can get the residuals 0, 1, 2, 3, 4, 5, and 6 we can express W in terms of factors of 7, 17 and 11 for big numbers of W. To answer the third and the fourth question we have to figure out which the big values are. I my analysis I use table 5 to construct table 6.
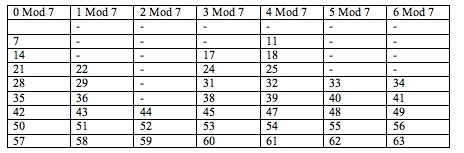
The empty cells mean that is not possible to buy exactly that amount of McNuggets using boxes of 7, 11 and 17
From the table 6 we are able to answer another question. The
largest number for which is impossible to purchase exactly number
of McNuggest is 37.
Further explorations
One interesting exploration is construct different set of
three or more numbers that allows students to form a well-defined
set for modular arithmetic (using different modules).