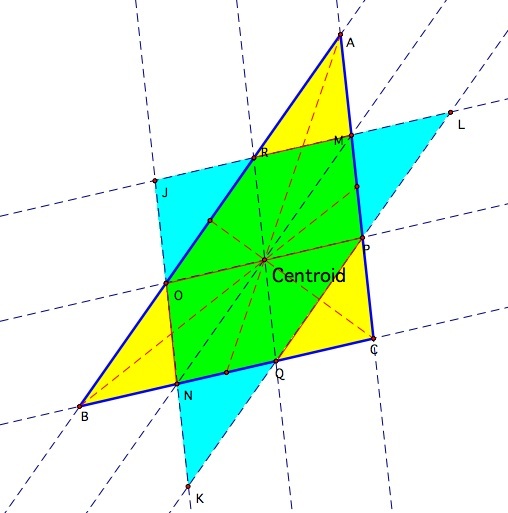
Barney is in the triangular room. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.

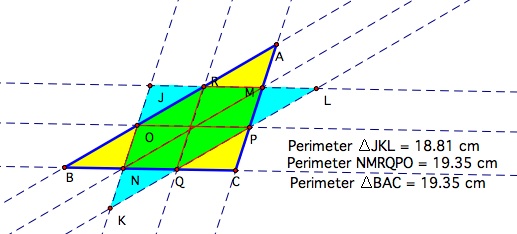
Explore yourself here

Because the line segments that Barney follows are parallel to opposite sides, similar triangles are formed within the triangular room. Since they have the same measure angles, the path that Barney takes always follows the same angle of the original triangle. Barney will always return to the same point at which he began. Barney will touch the walls five times before reaching the starting point.

We can also check using parallelograms to prove that the length of the path is equals to the perimeter of the triangle if the starting point is chosen in the segment BC. Using parallelograms each segment of the perimeter could be replaced by a segment in the path

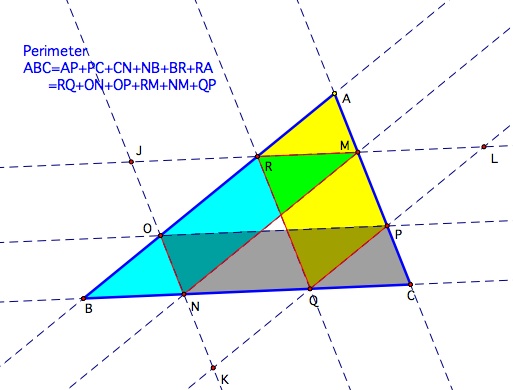
In contrast when the starting point is outside the segment BC, , the length of the path is equal to the perimeter plus twice the sum of the lengths of the segments AR, BO, and CP.

Notice that the new path generates parallelograms surrounding the triangle ABC where the segment MR = NB and so on.

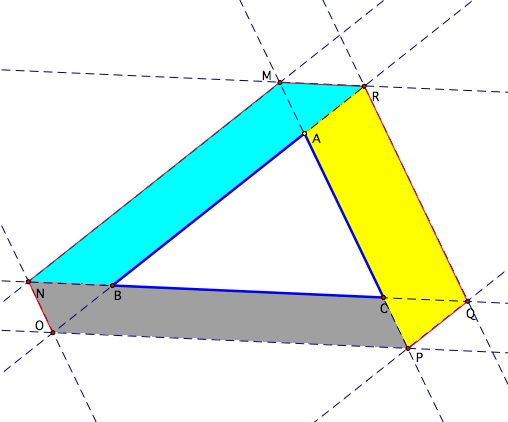
Another interesting result is that the figure ONMRQP is a non regular Hexagon when our point P is different from B and different from C. However, when our point is either B or C our figure is a triangle.

Other interesting result is that when our starting point is in the midpoint of the segment BC, the path goes three times through the centroid before reaching again the starting point. Besides, the length of the path will be equal to the perimeter of the medial triangle.

Return to my home page