Use of Graphs

Tonya C. Brooks

This whole semester, I have been wracking my brain for a situation in which people use mathematics outside of school. The problem is not that people don’t use mathematics, but how they use mathematics. My husband uses mathematics all the time in his job as a carpenter/deck builder. My mother uses mathematics often in her job as a GM seat manufacturer for Lear Corporation. Everyone uses mathematics in their everyday activities: paying the bills, balancing the checkbook, calculating up how much items will cost at the grocery store, etc. I looked through some previous essays that were written for this class. Some of the previous essays are extremely interesting. Especially the essay about farm irrigation; my grandparents are farmers in Missouri, and they have several different irrigation systems. However, my grandparents didn’t really worry about the mathematics involved in watering their fields. Most of their fields are not large enough to need more than one system, and many times, they water parts of the gravel roads surrounding the fields. I wanted to write about a type of mathematics that is used for everyday purposes but that requires something more than the basic arithmetic functions. This was the hard part.

Then I got to thinking about some of the problems that my father, brother, and uncle continuously deal with. You see, they drive for a living. As a matter of fact they all work for a company in Missouri called Jack Cooper, and Jack Cooper hauls all different kinds of vehicles (mostly GM vehicles though).

Our country runs on semi trucks. No matter where you go, you will see them. They run 24 hours a day, 7 days a week. Open any newspaper and you will see ads looking for truck drivers. I constantly see TV ads advertising truck driving jobs for companies. Today, you can see the truck driving trade being talked about on the news all the time due to high fuel prices, and many privately owned trucking companies cannot continue to run due to high fuel prices, high insurance, and low pay.

Now, to the real problem that my father, brother, uncle, and thousands of other truck drivers constantly struggle with. When you drive a truck for a living, you have to constantly worry about road access for the truck, especially with car haulers. Semi trucks are one of the tallest and longest vehicles on the road, which means that low bridges, bridges that have maximum weight capacities, narrow streets and many other issues cause major problems for semi trucks. Car haulers have to worry about this even more than other truck drivers because they are generally taller than most other trucks because of the vehicles that they carry (especially when they are carrying vans).

Due to all these obstacles, my father, brother, and uncle have to constantly monitor what obstacles they are going to run into on their way to a drop site. They have to be aware of whether there are low bridges on certain roads, whether they are too heavy for bridges on a certain route, and if they get lost, they have to know whether there is a route that will allow them to turn around. I know how important this is because there were several times that other Jack Cooper drivers were not aware of obstacles on their chosen route and did not realize that they would not fit under a bridge until they were almost there. By that time, it was too late to take a detour, and the driver had to pull over and wait for help to come or had to unload the truck, drive under the overpass and then reload the truck. In other words, mistakes like these cause major disasters and cost quite a bit of money for the company and employees. It is the driver’s responsibility to make sure that mistakes like this do not happen.

In order to look at a possible way to solve these types of problems, I have decided to use graphs to see possible routes that might be taken. I let towns be the vertices in my graph and let roads between the towns be edges connecting my different vertices together. In other words, an edge connects two vertices if and only if there is a highway connecting those two cities.

Let’s take a look at one particular example. Let’s say that we must run a load of vans from Wentzville, MO and our last drop is in Dallas, TX. We must also make other drops along the way in Little Rock, AR, and Austin, TX. Below you will see several possible routes to the different cities as well as a few other smaller towns along the way.

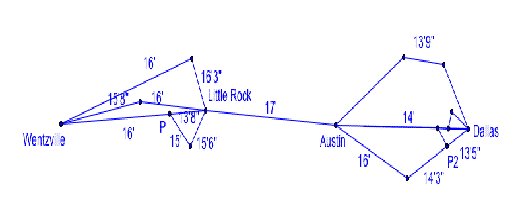
Let’s say that we are hauling a load of vans and that the height of the truck with the vans is 13’ 8”. In other words, we need to be aware of routes in which we encounter bridges that we cannot pass beneath. We can see in the example above that we have several different routes to choose from. We only see two roads that we cannot take, the one from P to Little Rock and P2 to Dallas.

Now, out of all the different routes that we have to choose from, we might prefer some over others. If we know that there is construction happening on certain highways, then depending upon the time that we will be passing through those areas, we might decide to go around and take a longer route because we think it might be faster and we will not have as much traffic. Also, I know that several times, my father and brother have taken longer routes simply because they do not want to have to pass through particular cities, such as Atlanta. They often plan their trips as they go along and try to schedule when they leave specific terminals or hotel rooms so that they reduce the amount of time that they spend in traffic, not only because they do not get paid for time in traffic, but because it has a higher risk for accidents, and many other reasons. On top of this, they also have to be mindful of other obstacles such as hills and mountainous areas due to the desire to keep their mileage rates high. Their trucks are regulated to run at most 62 miles an hour, which means that if they run into areas that require them to run up and down hills, or make lots of turns, their truck cannot keep the speed up and they end up doing a ridiculously slow speed. The company expects them to get so many miles per gallon of fuel, so they try to make sure that the routes they take are not going to jeopardize that. All of these factors go into the decisions that truck drivers make (and this just covers the issues if the truck is under the legal weight, log books are filled out correctly, and all other laws are obeyed).

Now, I know that if I said anything to my family about the use of graphs in order to find the best route to different places, they would all look at me as though I had lost my mind. However, what is nice about using graphs is that they are generally pretty simple and people use the ideas behind them all the time but do not realize it. People can use graphs such as the one above to determine the best way to deliver the mail and for work with circuits. Graphs can be used in today’s society by companies that help people find their soul mates, such as Match.com.

Graphs can also be used to determine how a company should fill the jobs that are open with the applicants. For example, let’s say that a company is looking for a carpenter, a plumber, an electrician, a landscaper, two painters, and two drywallers. They get applicants from 10 people. See the applicants below and the jobs that they are qualified for.

Applicant Qualified For

A Painter, drywaller

B Plumber

C Carpenter, landscaper

D Painter, plumber

E Electrician

F Electrician, plumber

G Drywaller

H Carpenter, Drywaller

I Landscaper, painter, electrician

J Electrician, drywaller

We can use graphs in order to show this situation. Let’s call our jobs J1 to J8. Our graph would look like:

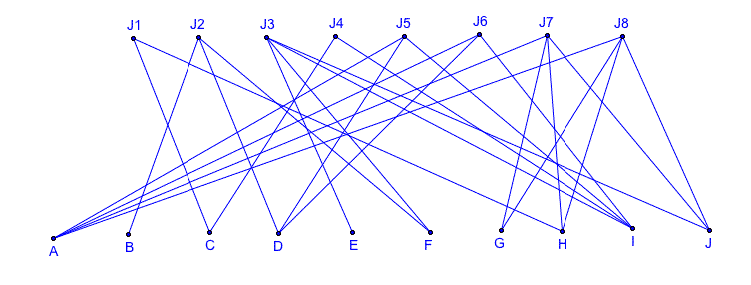
This looks pretty complicated, but we can test to determine if there is a possible way to cover all the jobs with the applicants. We will use the Hall’s Marriage Theorem which states: Let G be a bipartite graph with bipartition V(G) = X U Y. The following are equivalent:

1. The graph G has a maximum matching M that covers all of X.

2. For all S X, we have |S| ≤ |N(S)|.

In other words, we will be comparing the cardinality of S, with the cardinality of the neighbors of S. If the cardinality of S is larger than the cardinality of the neighbors of S for any subset S, then we cannot fill all the positions. Let’s look at an example. Let’s say that S consists of jobs J1 and J2. The neighbors of J1 and J2 are B, C, D, F, and H. Then |S| = 2 and |N(S)| = 5.

If we continue this for all the subsets of our jobs, we see that this is the case for all of our subsets of our set of jobs. We can go through in this case very easily and assign jobs to applicants. One such assignment is (J1, C), (J2, B), (J3, E), (J4, I), (J5, A), (J6, D), (J7, G), and (J8, H). Can you find any others?

Let’s take a look at a case in which we can’t find a matching that covers all of the jobs.

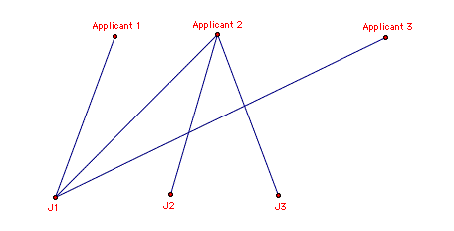
In this case, if we let our set S = {Applicant 1, Applicant 2}, then the neighbors of S = {J1}. In this case, |S| > |N(S)| and we cannot fill all of our jobs with the applicants.

Back to my page.