Find the Treasure!

Tonya C. Brooks

Problem: Two pirates decide to hide a stolen treasure on a desert island. There is a birch tree, which is directly west of a pine tree. They drive a stake into the ground between the two trees and the ocean. To bury the treasure, one of the pirates starts at the stake and walks towards the birch tree and after reaching the tree turns left 90 degrees and walks the same distance to another point. The second pirate starts at the stake and walks towards the pine tree, after which he turns right 90 degrees and walks that same distance to another point. The two pirates now advance towards each other and bury the treasure halfway between them. Several months later, the two pirates return to dig up the treasure only to discover that the stake was gone. Is it possible to devise a plan to find the treasure?

From the way that the problem is presented, it sounds like the placement of the stake is what is really important. Everything else depends upon where the stake is placed. To begin this problem, it might help us to get a handle on what happens to everything else when we change the placement of our stake. Let’s take a look at what things look like when we use Geometer’s Sketchpad to create our situation and look at how the placement of the treasure changes when we change the placement of our stake.

As you can see, when we move our stake around, the placement of the treasure doesn’t change! I found this to be quite a surprise!

So, the thing left to do is try to find exactly where this treasure location lies in respect to what we know.

We know where the two trees are, and that is about it. Everything else (other than the treasure) depends upon where the stake is placed. Let’s begin by creating a representation of our situation (much like we did with Geometer’s Sketchpad) and draw a line through our two trees.

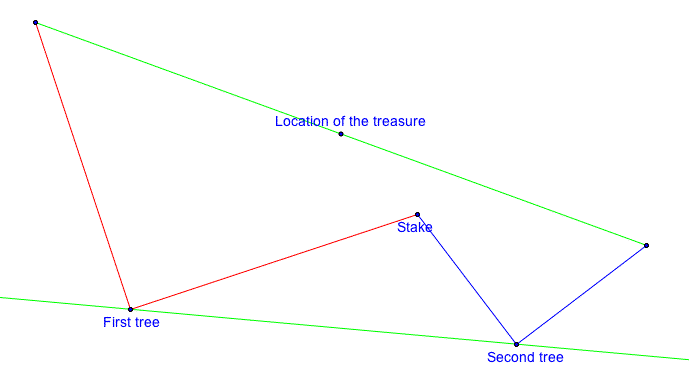
There are only a few things that we can do with this. My motto has always been to guess until something looks like it might turn out, and in this case, I would begin by drawing some new lines from the other points and the only lines that would be special are those that are perpendicular to our line through the two trees. Doing this we end with:

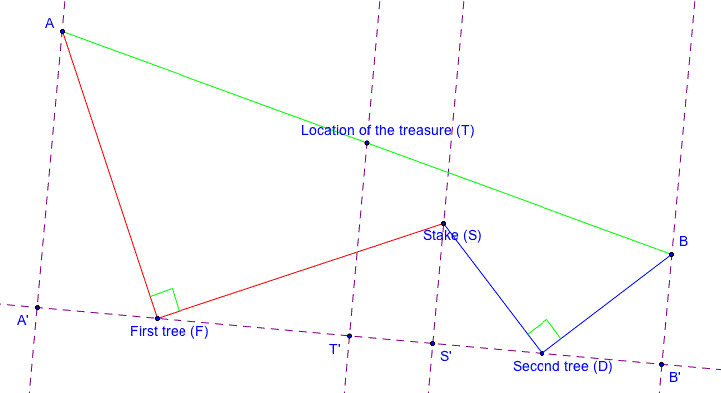
I claim that we have two sets of congruent triangles: AA’F and FS’S, and SS’D and DB’B. I will prove this claim later. For now, let’s assume that the triangles are congruent.

You will notice that our distance between the two trees can be written as FS’ + S’D. Because both FS’ and S’D are sides from the congruent triangles, we can say that FS’ + S’D = AA’ + BB’.

We also have that AA’B’B is a trapezoid in which the two base angles are right angles (because of perpendicularity). Also, the line TT’ is parallel to AA’ and BB’, and since T is the midpoint of AB, we can find the length of TT’ to be (AA’ + BB’)/2. Using the substitution FS’ + S’D in place of AA’ + BB’, we can find another equation for TT’ which is TT’ = (FS’ + S’D)/2.

Something that might help us is if we can determine exactly where T’ is located. If you notice, A’F = S’S = DB’. This tells us that A’T’ – A’F = T’B’ – DB’. Therefore, FT’ = T’D and T’ is the midpoint of FD.

Putting all this together, in order to find the treasure, we can go halfway between our two trees, turn ninety degrees to face the direction we need to go and then go the same distance we just went. Then it is time to dig up the treasure!

Now it is time to go back and prove the claim that all of this work is based on. Remember, the claim was that we had two sets of congruent triangles. Let’s look at just one, say, SS’D and DB’B. I claim that these two are congruent.

So, what do we know? Well for starters, we know that the angle measure of SDB is ninety because that was given to us. We also know that side SD is congruent to side DB, which was also given to us. By the fact that the lines SS’ and BB’ are perpendicular to the line S’B’ we know that we have right angles for angles SS’D and DB’B.

Let’s say that angle BDB’ has measure of q. Then angle SDS’ would be have a measure of 90 – q because the three angles seen must add to 180 degrees and we know that one of them has measure 90. Also, we are given two angle measures for our two triangles so we know that angle DSS’ has a measure of q. Using this, we can see that the cos(q) = [(measure of SS’)/(measure of SD)]. In the other triangle though, we have that the cos(q) = [(measure of DB’)/(measure of DB)] = [(measure of DB’)/(measure of SD)]. The two equations are both equal to the cos(q) and since q is restricted to being between 0 and 90 degrees, we can set the two equal to each other and see that measure of SS’ is equal to the measure of DB’. By SAS, the two triangles are congruent.

Back to my page.