
Final Projects
By Tonya C.
Brooks
For this project, I have worked on two problems. One is sometimes known to school
children as the Bouncing Barney problem and the other is known as CevaŐs
Theorem.
LetŐs look at the Bouncing Barney problem first. Say that we are given a triangle and we
choose a point on one side of the triangle. From this point, we move to another side of the triangle by
moving parallel to the other side.
If we continue this pattern, will we end up at the same point as we started? The answer is yes, and after six or
fewer travels or segments. LetŐs
take a look at what is going on.
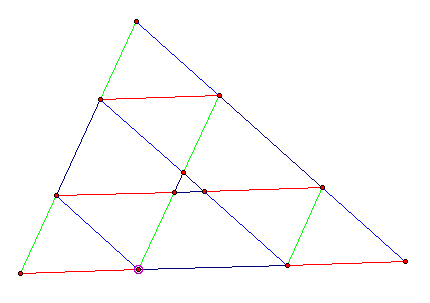
By
moving parallel to the sides of the triangles, we are generating a bunch of
parallelograms. We know quite a
bit about parallelograms that will help us with this problem. For instance, we know that opposite
sides are congruent and opposite angles are congruent. For example, we can say that ED, GJ and
CF are all congruent. We can use
this idea repeatedly to see that we end up with a set of triangles that are
congruent by SSS. Also, since GF
is parallel to AB and that we have two lines that cut these parallel lines, we
see that angle CFG is congruent to CBA and angle CGF is congruent to CAB. Since they share a common angle and
have one other in common, we see that triangles CFG and CBA are similar which
means that all the congruent triangles are similar as well. Using all of these ideas of
parallelograms, it is easy to see why we would end up at our same point after
just a few bounces (because our corner triangles are all congruent).
A
few different cases can come up.
There are a few places in which we end up with our three triangles with
boundaries formed by our path all meet in the middle of our triangle. We can see what can cause this by
looking at the segments created on just one side of the triangle ABC. One thing to notice is that each side
of ABC is segmented into thirds.
How many congruent triangles are created in this case?
Also, if you notice, when your point is chosen to be the midpoint of one
of the sides, we really have only four triangles inside ABC. Why do you think this is? Once again, you should be looking at
what goes on in parallelograms. If
you notice, each side of the triangle is bisected due to parallelograms.
What happens when we choose a point between thirds and midpoints? Take a guess and then take a look at
happens. Why do you think this
happens and can you use this to see what might be happening when our point
begins at the midpoint?
By looking at the sets of
congruent lines from above, you can add up the sides of ABC and see that the
sides add up to be the same distance that Barney will travel, except in the
case of when we start at the midpoint.
In this case, since we bisect each of the sides and our four triangles
are congruent, it is easy to see that the length Barney travels is exactly half
of the perimeter of ABC.
Once we begin looking at the properties of parallelograms, everything
else about this problem falls very neatly into place. We really only have to use the two previous properties of
parallelograms in order to investigate this problem, which might be one of the
biggest reasons that younger children can work this problem and understand how
it works.
CevaŐs Theorem
Consider any triangle ABC and select a point P inside the triangle. Draw lines AP, BP and CP extended their
intersections with the opposite sides to points D, E and F respectively. What can we say about (AF)(BD)(EC) and
(FB)(DC)(EA)?
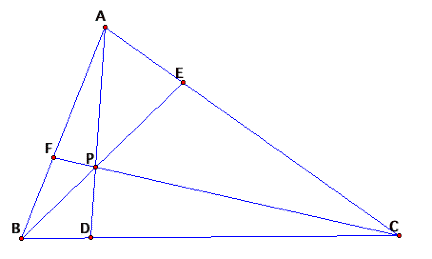
If
you noticed, my point P doesnŐt have to be any particular point, so we canŐt
say anything really specific about the inner triangles, so letŐs take a look at
what is happening with the areas of a few triangles.
LetŐs take a look at triangles BPD and CPD. In order to talk about areas of triangles, we usually use
base and height but if you notice, the height of these two triangles is the
same so letŐs call it x. Then, the
area of triangle BPD is (1/2)(BD)(x) and the area of CPD is (1/2)(CD)(x). We can use these two equations to see
what a ratio for (BD)/(CD) = Area (BPD)/Area (CPD).
LetŐs also look at two other triangles that have the same bases as these
two, namely triangles ABD and ACD.
These two also have the same height so letŐs call this height y. Then the area ABD is (1/2)(BD)(y) and
the area of triangle ACD is (1/2)(CD)(y).
We can also use these two to generate another equation for the ratio
BD/CD = Area (ABD)/Area (ACD).
LetŐs combine these two equations to get a new one for BD/CD which is
Area (APB)/Area (APC). We can do
the same for the other sides to see that AF/BF = Area (CPA)/Area (CPB) and
CE/AE = Area (BPC)/Area (BPA).
So
what does this have to do with anything?
LetŐs take a look at (BD)(AF)(CE)/(CD)(BF)(AE). When we do the multiplication of our
three ratios we end up getting one, therefore the when we add up all the
left-hand segments on the sides of our triangles we get the same length as if
we added all the right-hand segments.
Explore this idea for different P points. Look at some special cases for P such
as the orthocenter as well as what happens when P is outside the triangle.