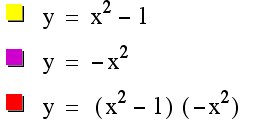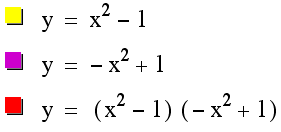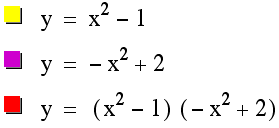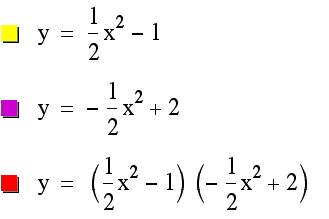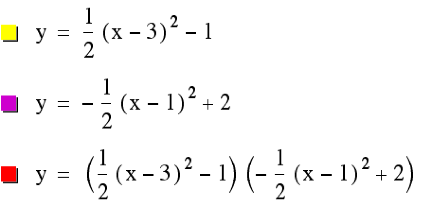The Product of Two Quadratic Functions and the Tangents They Create with Their Product.

By

Tonya C. Brooks

University of Georgia-Athens

In this assignment I want to examine what happens when we take two quadratic functions and multiply them together to get another fourth degree quadratic function, and how these all relate to one another. The goal for this project is to find two functions that will each have two points in common with their product and that the tangents be the same at these points.

Let us begin by looking at two very simple second degree quadratic functions x² and -x².

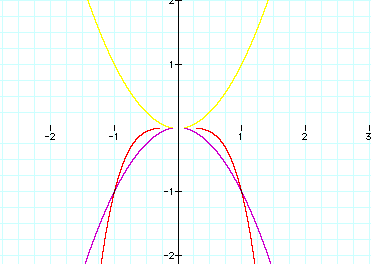
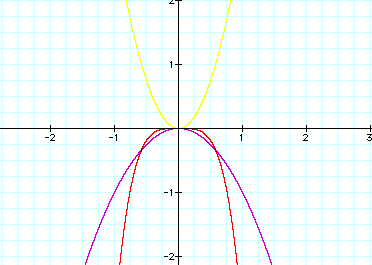
As you can see, the product of the two – the yellow x² and the violet –x² – gives us the red (x²)(-x²). Looking at the red, it looks as though it “bubbles out” a little on each side.

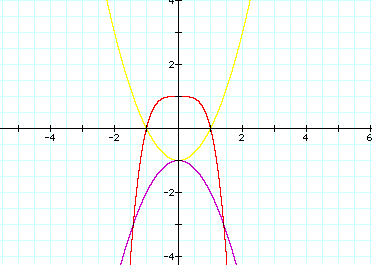
Let us take a look at what happens to the product if we have:

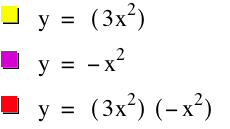
As you can see, we made the top one skinnier. However we weren’t able to get it any closer to the product’s graph in order to create a common tangent, so let’s try something else.

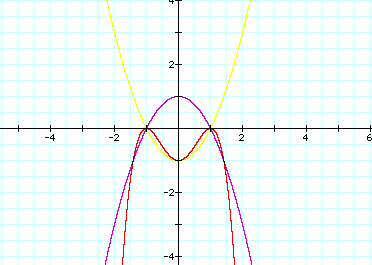
How about:

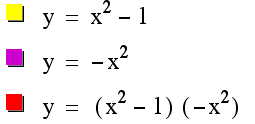
It is starting to look like we might be getting closer on our graph for –x², so let’s try something with that and leave our first equation as is since that is what caused brought our second and third mappings closer.

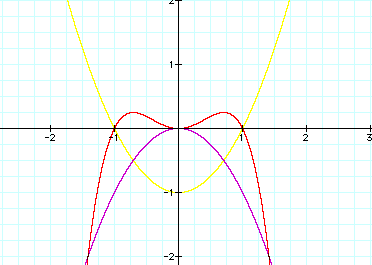
How about it we try:

That looks like it took us farther away from our goal for both equations, so let’s try:

That is really starting to look like something! Let’s make that change again and see what happens with:

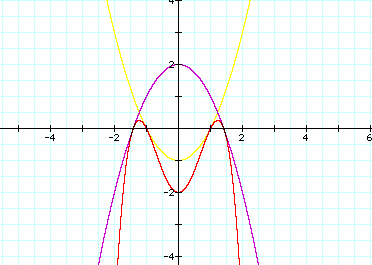
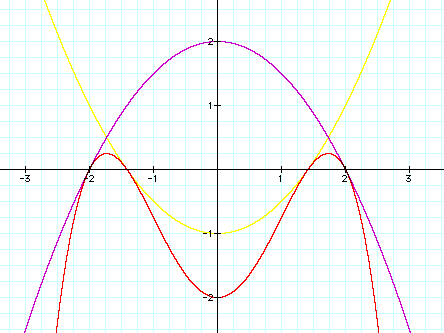
That looks pretty close, if not exact. Let’s go in for a closer look at the left side.

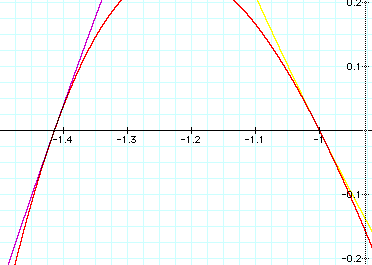
As you can see, it looks like both equations brush against the product and it looks like they have the same tangent line if we were to draw it in. If we take a close look at the right side, we would see a reflection of this.

From this, let’s take a look and see what happens if we change our multipliers for our x variable. Let’s try:

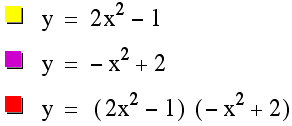
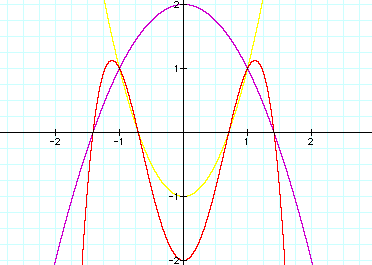
That doesn’t seem to work, so let’s try making the multipliers the same. As in:

So it seems as though we need to have our x multipliers be opposites in order for this to work.

How about shifting the graphs to the left and right? Is this okay or must we be centered on the y – axis? I would think that we would need to move both functions in the same direction the same amount but let’s look at what happens if we don’t follow this assumption. Let’s try:

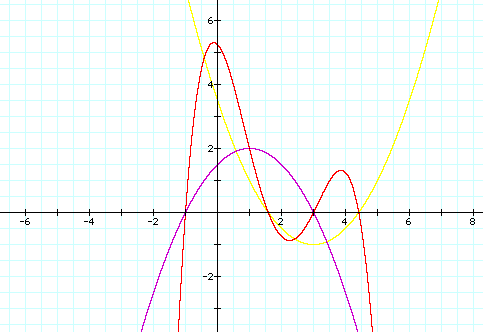
Whoa! We got some pretty wicked stuff but nothing that helps us with our problem so let’s try something else. How about:

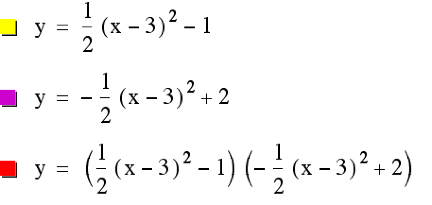
Okay, so it looks like we can shift the graph left and right without changing anything as far as sharing tangents is concerned. The next question we might ask is: Can we shift the graph up and down if we keep the distance between the critical points the same?

Click here to create your own set of equations to test your hypothesis.

Now, we have found two equations that do what we want, but if you notice, neither one of the equations deals with any x to the first power. Let’s look at what degree one does when we factor that in.

Look at what the relation is between x² +x - 1 and x² – 1.

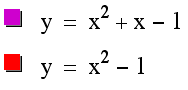
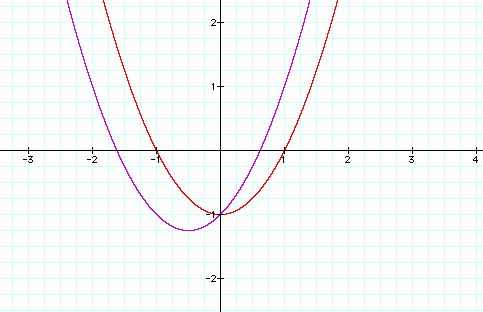
It looks as though that x in our first equation shifts our graph a little to the left and down. We might be able to create another set of equations with our desired property if we counteract the first x with a –x in our second equation. Let’s try with:

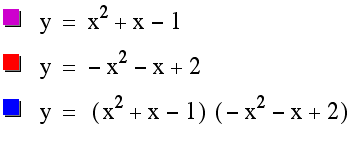
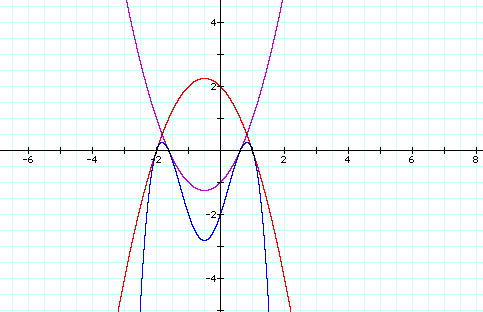
So, it is possible to create two second degree quadratic equations that are both tangent to their product in two places. The trick seems to be having opposite x² multipliers with the positive having a -1 y-intercept and the negative having a y-intercept value of 2, and opposite x multipliers.

Return.