Constructing Two Points on an Angle

By Tonya C. Brooks

Let’s take a look at what we are going to start with. We are given three random points, which we can use to create an angle. We are looking for a way to cut the sides so that the distance from our original two points is equal as well as being equal to the distance between our two created points. In other words, we want our picture to look something like this:

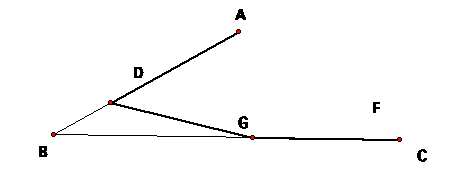
Let’s look at what we are given.

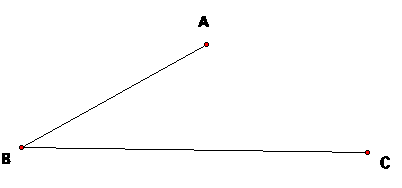
We will go with the good old mathematicians way of figuring something out. We will guess and hope we are correct. If we are wrong, then we will worry about that later. Hopefully something will come to us! Let’s pick some point D between A and B. Also, let’s draw a couple of circles centered at D and A with radius AD.

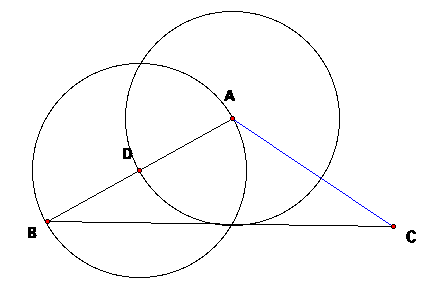
This doesn’t tell us much all by itself, but let’s work with our point D and a line parallel to BC.

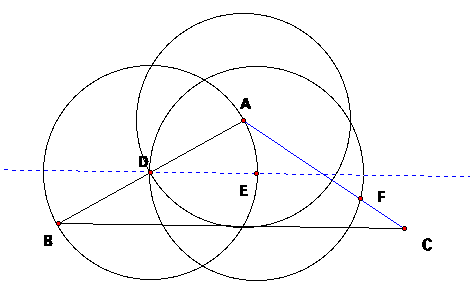
I called E the point where the circle around D intersects with our parallel line. Also, if we draw a circle around E with radius ED, we can see that this circle intersects AC at point F.

Let’s clear out our circles and notice that AD=DE=EF in the picture below (since our circles all had the same radius and these segments all go from the center of a circle to the outside of the circle).

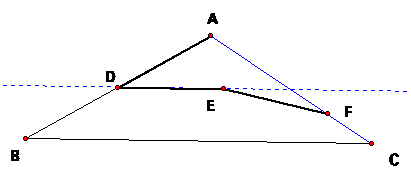
This still doesn’t look like much. The problem I see here, is if I move D around, E never falls on our segment BC at the same time as F, which is what we need to have happen. Let’s fix this by creating a parallel line through point F. Also, I need there to be a point G that is a reflection of E on this parallel line, so I create rhombus DEFG.

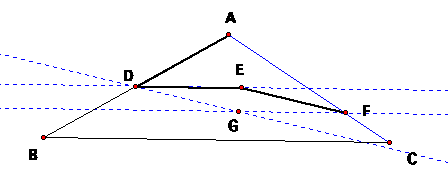
By construction, AD=DG=GF, so all we need to have happen is for G and F to fall on our segment BC. We can move point D around until this happens and we end up with:

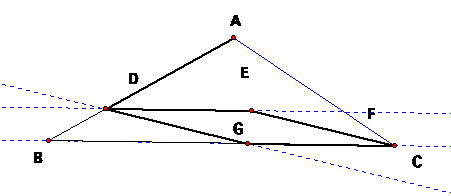
If we take out the segments we do not need, we end up with the picture from above.

Return.