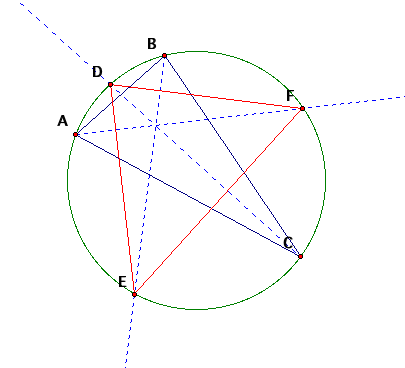
Circumscribed Triangles and Angles

By Tonya C. Brooks

In this assignment, I want to take a look at angles between two different triangles inscribed in a circle. These aren’t just any two triangles though. Let’s start with one inscribed in a circle and create another triangle inscribed in the same circle by taking the angle bisectors of the first and the intersection of these bisectors with the circle. We will use these points to create the second circle. We are going to figure out how the angles between these two relate.

In order to show how the angles relate to one another, we will need to use a theorem about a different case from what we see here. Consider the case below.

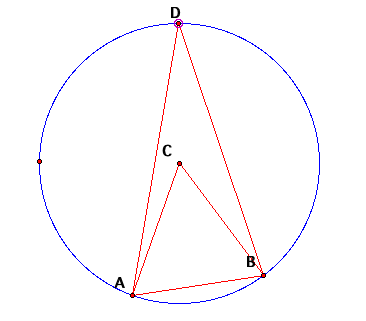
I claim that <ACB is 2<ADB. What I am saying is this: When we have two triangles that share the same chord of a circle, both triangles on the same side of that chord, and one triangle having the center of the circle as the third point and the other having a point on the circle, then no matter where the point is on the circle, the angle will never change.

Now this is obviously a big claim that needs to be proved, so let’s do this. Let’s connect points C and D.

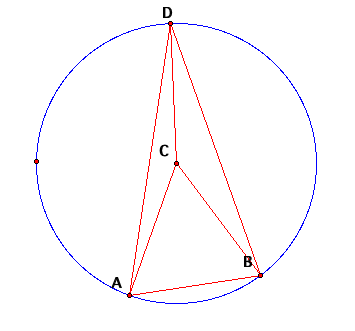
From construction, we have three different isosceles triangles. Let’s call <BDC = <DBC = x, <CDA = <DAC = y. Then <BCD = 180 – 2x, <ACD = 180 – 2y. We know that the total degrees around C add up to 360, therefore <ACB = 360 – (180 – 2x) – (180 – 2y) which simplifies to 2x + 2y. This is exactly two times <ADB (which was x + y). This proof works for cases that look like this (where the two triangles do not intersect), so let’s look at the other case.

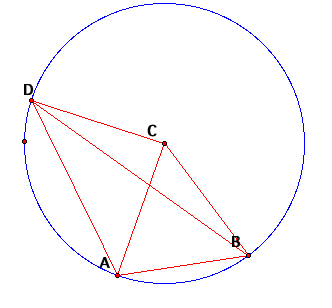
Once again, I have connected C and D. We still need to show that <ACB is 2<ADB. We have three isosceles triangles (ACD, ACB and DCB) so let’s label some of these angles. Let <BDC = <DBC = x. Let <DBA = y so that <BAC = x + y. Then <ACB = 180 – 2x – 2y. Also, let <BDA = z so that <DAC = x + z. Then from triangle DAB, we can see that z + (x + z) + (x + y) + y = 2x + 2y + 2z = 180. Therefore our <ACB = 2z which is two times <ADB, which is what we wanted to prove.

Let’s go back and take a look at our original problem now and use this outcome.

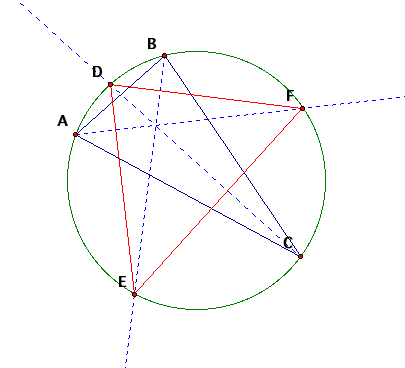
It is not apparent from this picture, but let me dissect a part for you to show you what I am going to do. Take a look at:

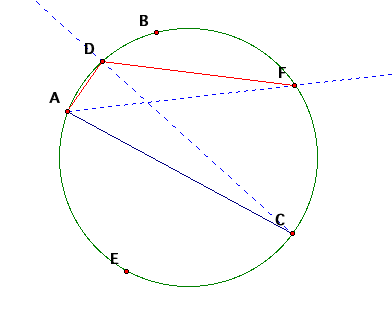
Without moving the points, I have erased all the lines that we are not going to use. I have also added in a segment (AD) to let you see how the theorem is going to be used. Triangles ACD and AFD both share a chord AD. From above, I can state that since C and F are on the circle on the same side that the angles are congruent. Using this idea repeatedly, we can see that the correlation goes as follows.

If we allow <A = 2x, <B = 2y and <C = 2z (since we constructed the other triangle from angle bisectors), then <D = x + y, <E = y + z, and < F = x + z.

The nice thing about using this proof is that as long as the requirements are met for the proof, then it doesn’t matter what kind of triangle you begin with.

Return.