Pedal Triangles

By Tonya Brooks

Before we begin to look at pedal triangles, it might be nice to know what they are. If we take the triangle formed from three lines and pick any point on the plane, we can construct a pedal triangle by taking perpendicular lines through our point to the three lines of the triangle. It might look something like this:

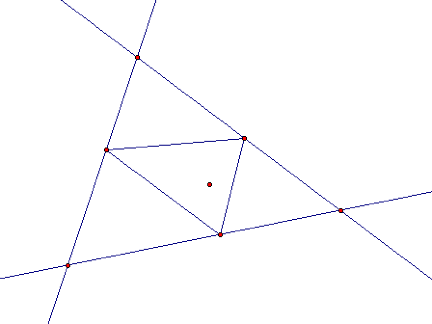
Now in this case, I let my point be inside the triangle but there is no reason that it needs to be (as we will see what happens when it is not). Also, for convenience, I have hidden the perpendicular lines.

Now let’s move our point around. One question we might consider is whether or not the point will always be inside the pedal triangle. We can see that if we move our point around, we actually can get times when the point is outside the pedal triangle. It happens when our construction looks something like this:

Did you notice that our point has moved outside our original triangle? One thing to notice is that when our point is on a side of our original triangle that it becomes one of the vertices of the pedal triangle. This seems to make sense since we take the points where our perpendicular line through our point intersects the lines of our triangle to create our pedal triangle.

Another thing to notice is what happens when our point is one of the vertices of our original triangle. As the point gets closer to the chosen vertex, the two sides of the pedal triangle that intersect the original triangle get closer and closer together until they eventually meet. At this point, everything comes together and our pedal triangle becomes a segment.

Do you notice anything about this segment? Well, from the way we constructed our triangle, the segment is perpendicular to the line for the triangle, and it goes through one of the vertices, therefore it becomes an altitude by definition.

As we continue to play with our point, we can see that at times our pedal triangle goes outside the original, like so:

By moving our point around, we can get the pedal triangle to be half in and half out of our original triangle or all the way outside as seen from above. It seems like our point just needs to be far enough out of our original triangle.

Return.