
Concurrence of
the Angle Bisectors of a Triangle
By Tonya Brooks
University of
Georgia
When we are working in geometry, it seems
like there are a lot of things that just seem obvious. When we are kids, we are able to draw things
out for ourselves and make assumptions that we donŐt have the liberty of making
as adults.
One of the many conclusions that we might
have made as kids is the intersection of the interior angles of a
triangle. We have been able to draw
several different triangles and have had the angle bisectors intersect in every
single one of them, but here I would like to show a formal proof.
Theorem: Let ABC be a triangle with angles A, B and C. We want to show that the angle
bisectors of A, B and C are concurrent.
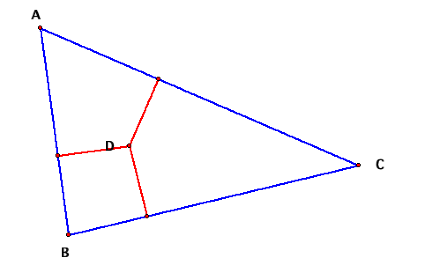
Proof: Let us bisect angles A and B. We can see that these two angle bisectors meet in a
point. LetŐs call this point D for
convenience.

What makes these points on the angle bisector
special? All of the points on the
angle bisector of A are equidistant to the two sides of angle A. This means that point D is equidistant
from ray AC and ray AB. Also,
since point D is on the angle bisector for angle B, D is equidistant to rays BA
and BC. LetŐs look at this info in
a diagram.
Now, I know I talked about D being
equidistant to the three rays AC, AB and BC. What does that mean for this? Think about it like this: When you are standing in a room and want to measure the
shortest distance to the wall, how do you measure? Most people would measure the shortest distance, which just
so happens to be the distance that creates a right angle with the wall. The point D is no different.
Here, the three red segments are the
shortest distances between D and the sides so they create right angles with the
sides of our triangle. Also, these
three are congruent.
We want to show that DC bisects angle
C. One of these segments we can
throw out. LetŐs see what we have.
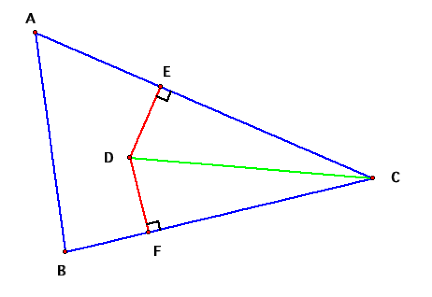
LetŐs look at triangles CDE and CDF. Notice that angles CFD and CED are
congruent, segments DE and DF are congruent and segment CD is congruent to
itself. By the Angle-Side-Side
theorem, the two triangles are congruent.
Therefore, CD is the angle bisector of angle C and the three angle bisectors
are concurrent.