Tangency Between 2 Linear Functions and Their Product

Assignment 1

Problem #3

By Erin Cain

In this problem I am asked to investigate the following:

Find two linear functions f(x) and g(x) such that their product

h(x) = f(x).g(x)

is tangent to each of f(x) and g(x) at two distinct points. Discuss and illustrate the method and the results.

I am sure that there are a variety of ways for one to approach this investigation, but I decided to begin with what I know. Since we are given that the two functions, f(x) and g(x), are both linear, I know that these functions will be written as :

f(x) = mx +b

g(x) = nx + c

where m and n are the slopes of the two functions and b and c are the y-intercepts of f(x) and g(x). When we multiply these two linear functions together to get h(x), we will get a polynomial of degree 2, i.e. a quadratic equation, which when graphed gives us a parabola. Now that we know this graph is a parabola, we also know that the graph has 2 roots (it crosses the x-axis twice)and they will most likely be where mx + b = 0 and nx + c = 0. This also tells us that h(x) will cross the x-axis when f(x) crosses the x-axis and when g(x) crosses the x-axis, therefore, if there is a point of tangency between these graphs it will be where they both cross the x-axis.

In order to start the actual investigation, I picked two arbitrary values for m, n, b, and c. In order to keep it a little less complicated, I made all of the values natural numbers. I let m=2 and b=1, f(x) = 2x + 1, and n=3 and c=4, g(x) = 3x + 4. Using the program Graphing Calculator, I graphed the functions f(x), g(x), and h(x) = (2x + 1)( 3x + 4). The graph is below:

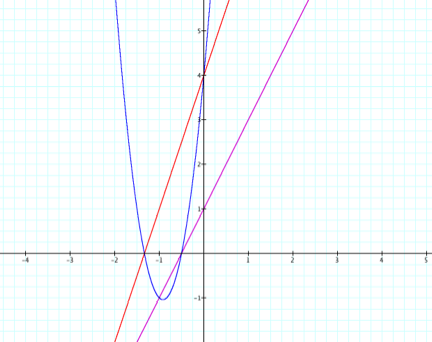
From looking at the graph, the first thing that you notice is that f(x) and g(x) are not tangent to h(x), the parabola. Therefore we need to re-think what numbers we use. When we think about the standard parabola, y = x², the tangent lines fall on opposite sides of the parabola.

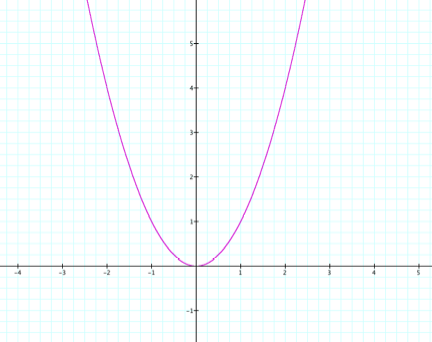
From the picture, we can also notice that if the tangent lines are on the opposite sides of the parabola, one of the tangent lines must be slanting upward, in other words as the x values increases the y value also increases, and the other tangent line must be slanting downward, in other words as the x value increases the y value decreases. This can be translated into talking about slope; when one line is slanting upwards it has a positive slope and when a line is slanting downwards it has a negative slope. Therefore, the lines f(x) and g(x) must have opposite slopes in order for us to find two linear equations whose product is a parabola that is tangent to lines.

Now lets try our last equations of f(x) and f(x) with opposite slopes. So this time f(x) = 2x + 1, g(x) = -3x + 4, and h(x) = (2x +1)( -3x + 4).

Once again, this did not produce what we were hoping for, but one thing did change. With allowing the slopes to have opposite signs, this caused our h(x) to become a completely different parabola. Our new parabola is now opening downward and it moved up and to the right where our maximum point has a positive x and y value.

Lets now see what happens when we allow our y-intercepts to be the same number, i.e. b = c. This time we will change both of our y-intercepts so that they both equal 3.5, but keep the rest of our two equations the same. Now we are graphing f(x) = 2x + 3.5, g(x) = -4x + 3.5, and h(x) = (2x + 1)(-4x + 3.5). Let’s see what happens:

This time we can see that 3.5 is possibly too large of a value for our y-intercepts. We know this because in order to have our lines f(x) and g(x) tangent to the parabola, our y-intercept must be above the maximum point of the parabola. Therefore we need to lower the value we use for our y-intercepts. What happens when we change our y-intercepts equal to 1?

Our y-intercept is now getting closer to where we want it. Let’s leave the y-intercept alone for a minute and see what happens when we change our slope. Let’s let the slopes of our lines be exact opposites of each other. This in turn will give us opposite forms of the same lines. Let’s begin by making our slopes 4 and -4. The graph will then look like this:

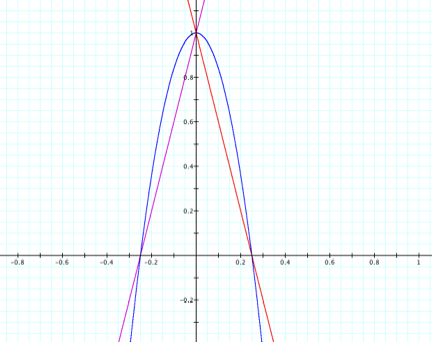
We are now getting much closer to what we are looking for. By changing the slopes and making them equal with the exception of the sign of the slopes, the lines f(x) and g(x) are on opposite sides of the parabola, but they cross the parabola at two points; hence the parabola is not tangent to the lines. What if we decrease the slope by 1?

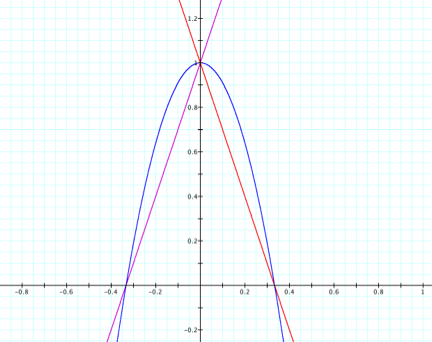
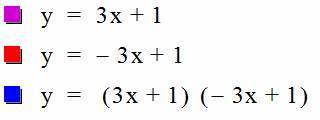
We are getting closer!!!! Since we are so close, let’s try changing the y-intercept again, but only change it on one of the equations. Currently our y-intercept is at 1, so lets cut it in half and make it ½.

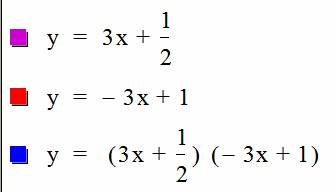
The lines are becoming closer to being tangent, so let’s make the other y-intercept equal ½ as well.

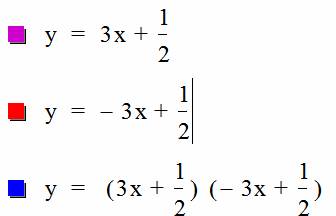
From first look, it looks like we have found two linear equations whose product is tangent tithe two lines. We need to do some careful examining to make sure this is correct. We can first check that the parabola is actually tangent to the lines by zooming in on both sides of the parabola.

The Right Side:

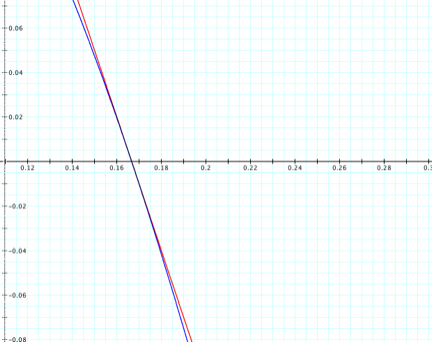
The Left Side:

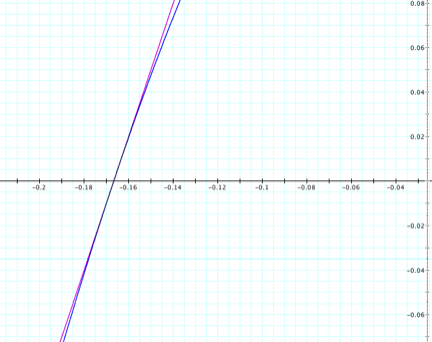
Looking at the zoomed in pictures, we can see that the parabola is tangent to the lines when f(x) = 0 and when g(x) = 0. We can also check this by looking at our equations when the slopes are equal to 1 and-1. Therefore we will have f(x) =x + ½ and g(x) = -1 + ½ . The graph will look like the following:

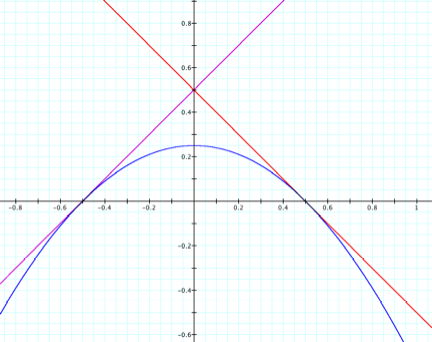
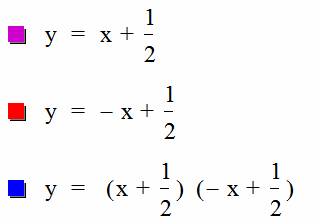
Once again, we can see that the function h(x) is tangent to the lines f(x) and g(x). As discussed at the beginning of this solution, the point of tangencies are where f(x) and g(x) cross the x-axis. Therefore we can graph these two different solutions on the same coordinate system.

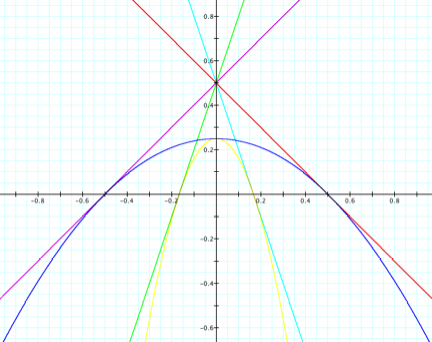
Looking at the above graph, we notice some similarities between ALL 6 of the graphs. This is that they all share the same line of symmetry, the y-axis. We can hypothesis now that the graph of the product, h(x), of two linear equations, f(x) and g(x), is tangent to the two linear equations as long as f(x) and g(x) have opposite slopes. It is important to note that it does not necessarily have to have the same y-intercept. If the y-intercepts are different, this means that they have a different line of symmetry besides the y-axis. For example, lets look at f(x) = (x – 2) + ½ and g(x) = -(x – 2) + ½.

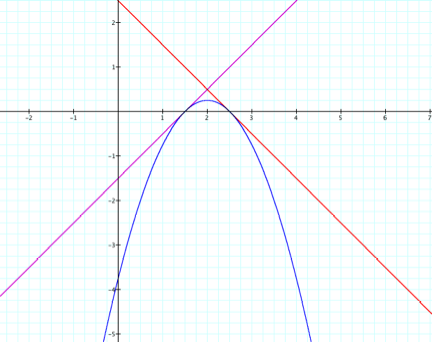
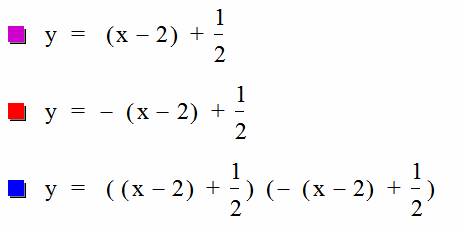
Here we have two functions, f(x) and g(x) that have opposite slopes and look like they have the same y-intercept. If we use the distributive property, we end up with f(x) = x – 3/2 and g(x) = -x +5/2. Now it is clear from the functions and the above graph that they do not have the same y-intercept, but because the slopes are opposite of each other, they still have the same line of symmetry. In this case it looks to by x = 2.

Therefore, we can generate numerous functions f(x) and g(x) where their product is tangent to each linear function as long as they have opposite slopes, m and –m, and the line of symmetry for h(x) and the two linear functions is parallel to they-axis.

RETURN